정규화 : 희소성 (Regularization for Sparsity)
다차원의 특성 벡터에 대해 학습된 모델의 특수 요구 사항에 대해 알아보자.
L1 정규화 (L1 Regularization)
희소 벡터는 종종 여러 차원을 포함한다. 거기에 특성 교차를 생성하면 더 많은 차원이 생긴다. 이러한 고차원 특성 벡터가 주어지면, 모델의 크기가 커지고 엄청난 양의 RAM이 필요할 수 있다.
고차원 희소 벡터에서, 가능하다면 가중치를 0으로 낮추는 것이 좋다. 정확히 0의 가중치는 필연적으로 해당 특성을 모델로 부터 제거한다. 특성을 0으로 설정하면 RAM이 절약되고, 모델의 노이즈가 줄어들 수 있다.
예를 들어, 캘리포니아 뿐만 아니라 전 세계를 포괄하는 주택 데이터 세트가 있다고 가정하자. 전 세계의 위도를 ‘munite level’(도당 60분)로 bucketing하면 약 10,000개의 차원이 추가로 생긴다. 경도도 같은 방식으로 진행하면 20,000개의 차원이 추가로 생긴다. 거기에 더해 이 두 특성의 특성 교차는 약 2억 개의 차원이 생긴다. 하지만, 이 2억 개의 차원 중 많은 부분은 사람이 살 수 없는 지역(예: 태평양 한 가운데)을 나타내기 때문에, 일반화하기 어렵다. 이러한 불필요한 차원을 저장하는데에 RAM의 비용을 지불하는 것은 어리석은 짓이다. 따라서, 무의미한 차원에 대한 가중치는 정확히 0으로 낮추는 것이 좋다. 그렇게 되면 추론 시간에 쓸데없는 모델 계수의 저장 비용을 지불하지 않아도 된다.
그렇다면 어떻게 할 수 있는가? 불행히도, 앞에서 공부한 L2 정규화는 가중치를 작게 만들 수는 있지만 정확히 0으로 강제하지는 못한다.
다른 아이디어는, 모델에서 0이 아닌 계수의 개수에 패널티를 주는 정규화 항을 생성하는 것이다. 이 수를 늘리는 것은 데이터에 맞추는 모델의 능력에 충분한 이득이 있는 경우에만 정당화된다. 불행히도, 이 개수 기반 접근 방식은 직관적으로는 매력적이지만, 볼록 최적화 문제를 비볼록 최적화 문제로 전환한다. 따라서, L0 정규화로 알려진 이 아이디어는 실제로 효과적으로 사용할 수 없다.
그러나, L0 정규화와 비슷하지만 볼록하므로 계산에 효율적이라는 이점을 가지고 있는 L1 정규화가 있다. L1 정규화를 사용하여 모델의 정보가 없는 많은 계수들을 정확히 0이 되도록 만들 수 있으므로 추론 시간에 RAM을 절약할 수 있다.
L1 regularization vs. L2 regularization
L2 와 L1은 가중치에 다르게 페널티를 부과한다.
- L2는 가중치의 제곱에 페널티를 부과한다.
- L1은 가중치의 절대값에 페널티를 부과한다.
결과적으로, L2 와 L1은 서로 다른 도함수를 갖는다.
- L2의 도함수는 2 * 가중치
- L1의 도함수는 k (값이 가중치와 무관한 상수)
L2의 도함수를 매번 가중치의 x%를 제거하는 힘으로 생각할 수 있다. Zeno에서 알 수 있듯이, 수 십억 번 x%를 제거하더라도 감소되는 숫자는 0에 도달하지 않는다. L2는 일반적으로 가중치를 0으로 만들지 않는다.
L1의 도함수는 매번 가중치에서 상수를 빼는 힘으로 생각할 수 있다. 그러나 절대값 덕분에 L1은 0에서 불연속성을 가지므로 0과 교차하는 빼기의 결과는 0이 된다. 예를 들어, 빼기로 인해 가중치가 +0.1에서 -0.2로 강제로 변경되면, L1은 가중치를 정확히 0으로 설정한다.
모든 가중치의 절대값에 페널티를 주는 L1 정규화는 넓은 모델에 대해 매우 효율적인 것으로 확인되었다.
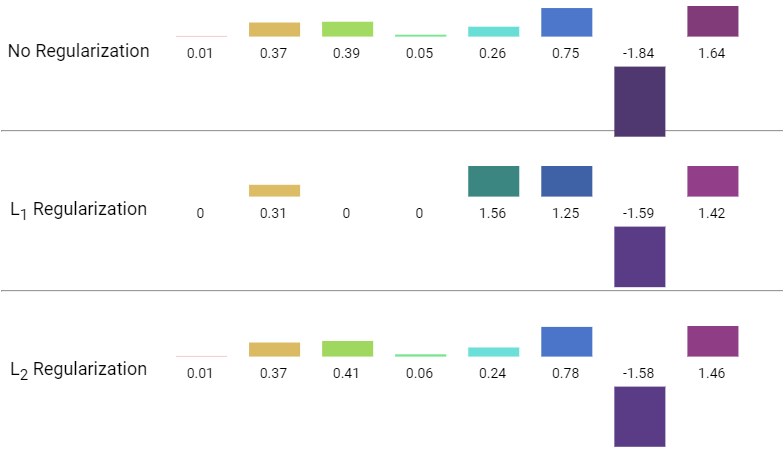
아래의 그림은 정규화 없음, L1 정규화, L2 정규화가 가중치 네트워크에 미치는 영향을 비교하기 위해 각각의 결과를 나타낸 것이다.
※ 참고
