신경망 (Neural Networks)
신경망은 특성 교차보다 더 정교한 버전이다. 본질적으로, 신경망은 적절한 특성 교차를 학습힌다.
구조 (Structure)
전에 공부했었던 특성 교차로 부터 회상하면, 아래의 분류 문제는 비선형이다.
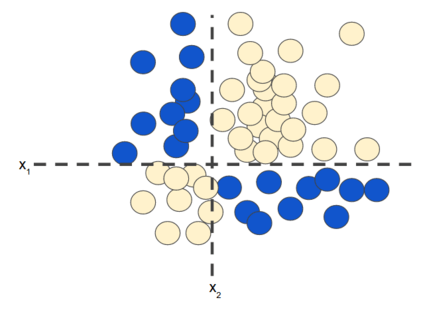
‘비선형’은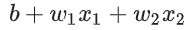 
형식의 모델로는 label을 정확하게 예측할 수 없다는 것을 의미한다. 즉, ‘결정 표면’은 직선이 아니다. 이전, 비선형 문제를 모델링하는 한 가지 가능한 접근 방식으로 특성 교차를 살펴보았다.
다음의 데이터 세트를 보자.
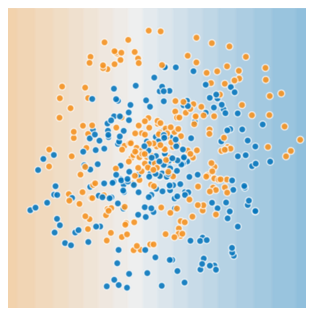
위의 데이터 세트는 훨씬 더 어려운 비선형 문제이다. 선형 모델로는 해결할 수 없다.
신경망이 비선형 문제에 어떻게 도움이 되는지 알아보기 위해 선형 모델을 그래프로 나타내는 것부터 시작해보자.
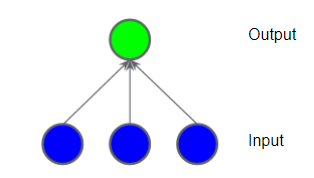
각 파란색 원은 입력 특성을 나타내고, 녹색 원은 입력 값들의 가중치의 합을 나타낸다.
비선형 문제를 다루는 능력을 향상시키기 위해 이 모델을 어떻게 변경할 수 있을까?
은닉층 (Hidden Layer)
아래의 그림으로 표시되는 모델에서, 중간 값의 ‘은닉층’을 추가했다. 은닉층의 각 노란색 노드는 파란색 입력 노드 값들의 가중치 합이다. 출력은 노란색 노드들의 가중치의 합이다.
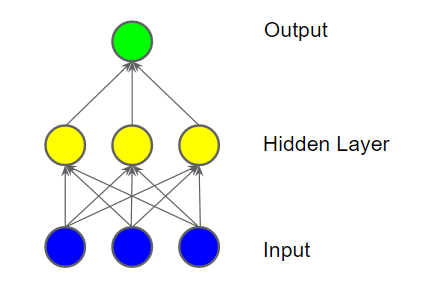
그렇다면, 은닉층이 추가된 위 모델은 선형인가? 그렇다. 출력은 여전히 입럭의 선형 조합이다.
아래는 두 번째 은닉층을 추가했다.
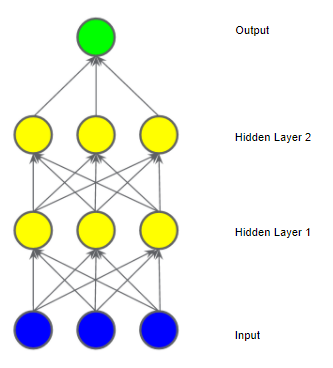
이 모델은 어떤가? 여전히 선형인가? 그렇다. 출력을 입력의 함수로 표현하고 단순화하면 입력의 또 다른 가중차의 합을 얻게 된다. 이 합계 역시 위의 데이터 세트의 비선형 문제를 효과적으로 모델링하지 못한다.
활성화 함수 (Activation Function)
비선형 문제를 모델링하기 위해서, 비선형성을 직접 도입할 수 있다. 비선형 함수를 통해 각 은닉층 노드를 송신할 수 있다.
아래의 그림과 같은 모델이 있다. ‘Hidden Layer 1’의 각 노드의 값은 다음 레이어의 가중치의 합으로 전달되기 전에 비선형 함수에 의해 변환된다. 여기서의 비선형 함수를 활성화 함수라고 부른다.
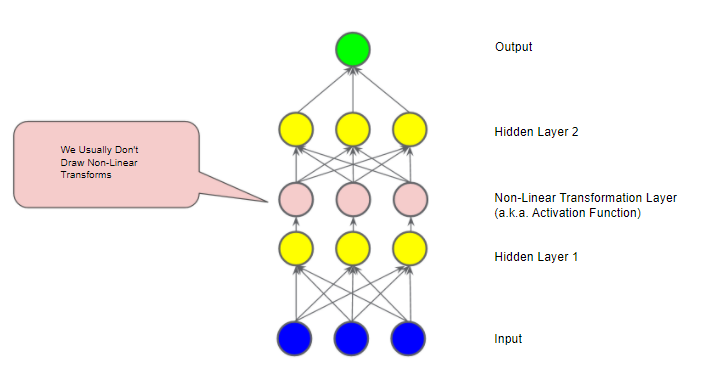
활성화 함수를 추가함으로써, 레이어를 추가하는 것은 더 큰 영향을 미친다. 비선형성에 비선형성을 쌓는 것은 입력과 예측 출력 사이의 매우 복잡한 관계를 모델링할 수 있다. 간단히 말해서, 각 레이어는 원래의 입력값에 대해 더 복잡하고 더 높은 수준의 기능을 효과적으로 학습한다. 이 원리에 대해 더 자세히 알고 싶다면 Chris Olah의 기술블로그를 참고하면 좋다.
대표적인 활성화 함수 (Common Activation Functions)
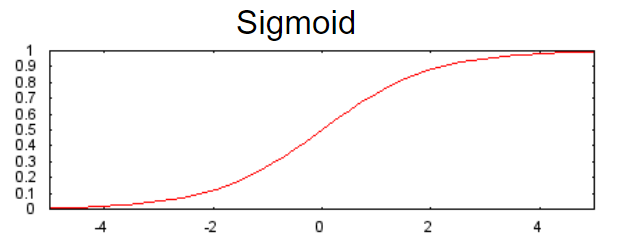
- 시그모이드 (Sigmoid) 함수는 가중치 합을 0과 1사이의 값으로 변환한다.
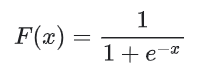
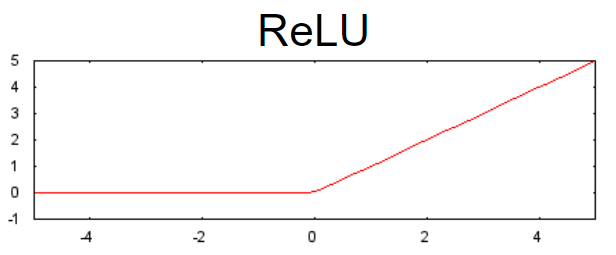
- ReLU (Rectified Linear Unit) 함수는 종종 시그모이드와 같은 평활 함수보다 약간 더 성능이 좋고, 또한 계산도 훨씬 쉽다.
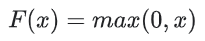
ReLU의 우월성은 경험적 발견을 기반으로 하며, 아마도 ReLU가 보다 반응성에서 유용한 범위를 가지고 있기 때문일 것이다. 시그모이드의 반응성은 양쪽에서 상대적으로 빠르게 떨어진다.
사실, 어떤 수학 함수라도 활성화 함수로 사용될 수 있다.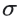 
는 활성화 함수를 나타낸다. 결과적으로 네트워크 안에서 노드의 값은 다음의 공식에 의해 계산된다.
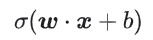
요약 (Summary)
‘신경망(Neural Network)’이라는 것은 표준 구성 요소를 가지고있다.
- 뉴런과 유사한 노드의 집합은 레이어 안에 구성된다.
- 가중치 세트는 각 신경망 레이어와 그 아래에 위치한 레이어 간의 연결을 나타낸다. 아래 계층은 다른 신경망 레이어이거나 다른 종류의 레이어일 수 있다.
- 편향 집합은 각 노드에 대해 하나이다.
- 활성화 함수는 레이어에 있는 각 노드의 출력값을 변환한다. 레이어가 다르면 활성화 함수도 다를 수 있다.
신경망이 항상 특성 교차보다 더 나은 것은 아니지만, 신경망은 많은 상황에서 잘 동작하는 유연한 대안을 제공한다.
※ 참고