Kyoungtae Min

진화하는 엔지니어가 되기 위한, 공부 내용 정리 및 기록

2 분 소요

로지스틱 회귀(Logistic Regression)는 정확하게 0 또는 1을 예측하는 대신, 0과 1사이의 확률을 생성한다. 예를 들어, 스팸 메일 탐지를 위한 로지스틱 회귀 모델이 있다고 가정해보자. 모델이 특정한 메일에 대해서 0.932의 값을 추론했다면, 이 메일이 스팸일 확률이 93.2% 라는 것을 의미한다.

확률 계산 (Calculating a Probability)

많은 문제가 확률 추정치를 출력으로 요구한다. 로지스틱 회귀는 확률 계산에 매우 효율적인 메커니즘이다. 실제로 다음 두 가지의 방법으로 추론된 확률을 사용할 수 있다.

  • 확률 그 자체로서 사용
  • 이진 범주로 변환하여 사용

그럼 첫 번째로, 확률을 그대로 사용할 수 있는 방법을 알아보자. 한밤중에 개가 짖을 확률을 예측하기 위한 로지스틱 회귀 모델을 만든다고 가정하자. 그 확률은 다음과 같다.


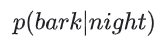
로지스틱 회귀 모델이 예측한 확률이 0.05라면, 1년에 약 18번은 개가 한밤중에 짖을 것으로 예상할 수 있다.


다음은 두 번째 방법인, 이진 범주로 변환하여 사용하는 방법을 보자. 이 방법의 목표는 두 개의 label(예: ‘스팸이다’ 또는 ‘스팸이 아니다’) 중 하나를 정확하게 예측하는 것이다.

로지스틱 회귀 모델이 어떻게 항상 0 과 1 사이의 값을 출력으로 보장할 수 있는지 궁금할 것이다. 이 때는, 다음과 같이 정의된 시그모이드(sigmoid)함수를 사용한다. 시그모이드 함수는 동일한 특성을 같은 출력을 생성한다.


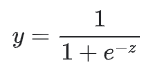
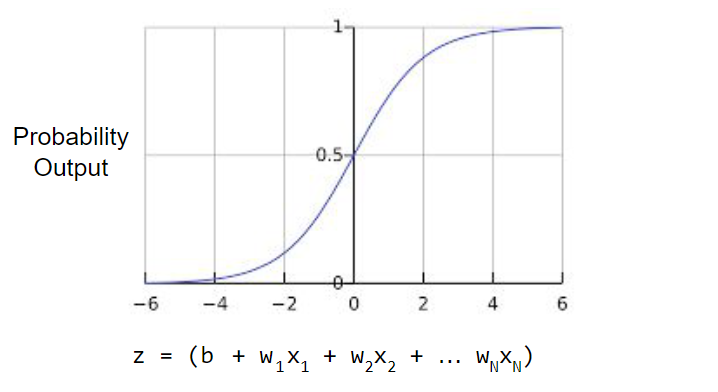
시그모이드 함수를 그래프로 표현하면 다음과 같다.

Sigmoid Function


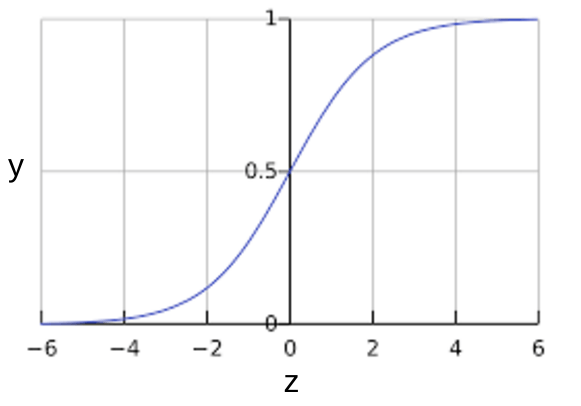
z가 로지스틱 회귀로 학습된 선형 레이어(layer)의 출력을 나타내는 경우, sigmoid(z)는 0 과 1 사이의 값(확률)을 산출한다. 수학적으로 표현하면 다음과 같다.


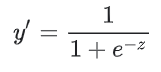
  • y’ 특정 데이터에 대한 로지스틱 회귀 모델의 출력이다.
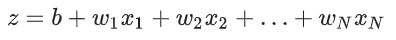
    • w는 모델의 학습된 가중치이며, b는 편향이다.
    • x는 특정 데이터에 대한 특성값이다.

시그모이드의 역함수는 z가 레이블1(‘개가 짖을 것이다’)의 확률을 레이블0(‘개가 짖지 않을 것이다’)의 확률로 나눈 것의 로그로 정의될 수 있다고 명시하기 때문에 ‘log-odds라고도 불린다.



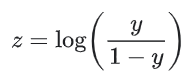
세 가지 특성을 가지고, 아래와 같은 편향과 가중치를 학습한 로지스틱 회귀 모델이 있다고 가정하자.


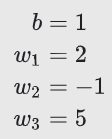
또한 주어진 데이터는 다음과 같은 특성값을 가지고 있다면,


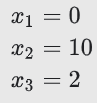
log-odds의 계산은,


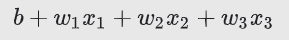
따라서,


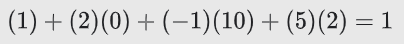
log-odds값을 시그모이드 함수에 대입하면, 결과적으로, 주어진 데이터에 대한 로지스틱 회귀 예측값은 0.731이 된다.



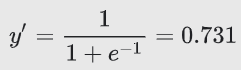
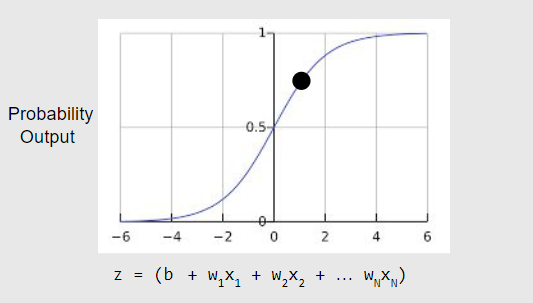
최종적인 예측 확률은 73.1%이다.

Loss and Regularization

Loss function for Logistic Regression

선형 회귀(linear regression)에 대한 손실 함수(loss function)는 손실 제곱(squared loss)이다. 로지스틱 회귀에 대한 손실 함수는 Log Loss이다.


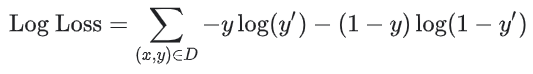
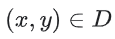  • 은 (x, y)로 쌍을 이루는 데이터 세트이다.
  • y는 레이블이 지정된 데이터의 레이블이다. 로지스틱 회귀이므로 y의 모든 값은 0 또는 1이어야 한다.
  • y’는 주어진 x의 특성들에 대해 예측된 값(0과 1사이)이다.

Regularization in Logistic Regression

정규화(Regularization)는 로지스틱 회귀 모델링에서 매우 중요하다. 정규화가 없으면, 로지스틱 회귀의 점근적 특성은 loss를 고차원에서 0으로 계속 몰아간다. 결과적으로, 대부분의 로지스틱 회귀 모델은 모델 복잡도를 줄이기 위해 다음 두 가지 전략 중 하나를 사용한다.

  • L2 Regularization
  • Early stopping(학습 횟수 또는 learning rate를 제한)

(좀 더 뒤에서 L1 Regularization에 대해서도 다룰 것이다.)

각 데이터에 고유한 ID를 할당하고, 각 ID를 고유한 특성으로 매핑한다고 가정해보자. 정규화 함수를 명시하지 않았다면 모델은 완전히 과대적합될 것이다. 왜냐하면, 모델은 모든 데이터에 대해서 loss를 0으로 만들려고 하지만 절대 그렇게 되지 못하기 때문에 각 지표 특성에 대한 가중치를 ‘양의 무한’ 또는 ‘음의 무한’으로 유도하기 때문이다. 이는 각각 하나의 데이터에서만 발생하는 엄청난 양의 특성 교차(feature cross)가 있는 고차원 데이터에서 발생할 수 있다.

다행히 L2 정규화를 사용하거나 early stopping을 사용하면 이 문제를 방지할 수 있다.




※ 참고

Google Developer - Calculating a Probability
Google Developer - Loss and Regularization

참고