일반화 (Generalization)
Overfitting의 위험성 (Peril of Overfitting)
이번에는 일반화에 대해서 알아보자. 이에 대한 직관력을 기르기 위해 세 개의 산점도를 통해 알아볼 것이다. 각 그림에는 두 가지 색의 점들이 있는데,
- 파란색 : 병든 나무
- 노란색 : 건강한 나무
[그림1] 병든 나무와 건강한 나무
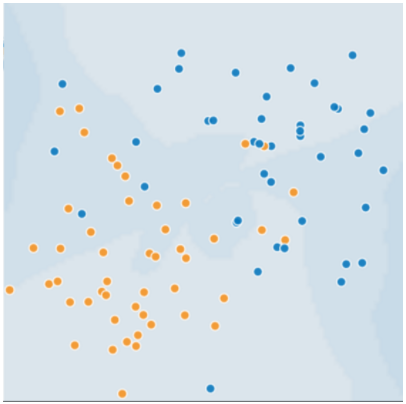
병든 나무와 건강한 나무를 예측하기 위한 좋은 모델을 상상할 수 있는가? 속으로 파란 점들과 노란 점들을 나누는 선을 그려보고 아래의 그림과 비교해 보자.
[그림2] 모델이 예측한 결과
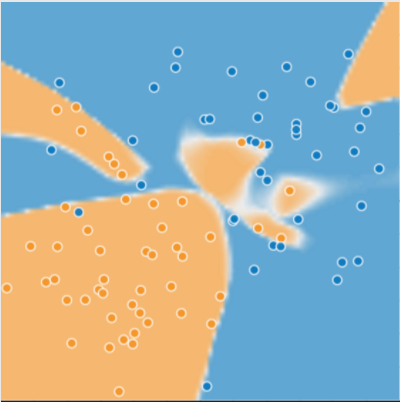
위 그림의 모델은 매우 작은 loss로 학습이 끝난 모델이다. 언뜻 보기에는 건강한 나무와 병든 나무를 잘 구분한 것처럼 보인다. 정말 그럴까?
Loss가 작아도 부정확한 모델일 수 있다?
아래의 그림은 모델에 새로운 데이터를 추가 예측 시켰을 때의 결과이다. 상당히 많은 부분을 잘못 분류하여 매우 저조한 성능을 보인 것을 확인할 수 있다.
[그림3] 새로운 데이터에 대한 예측 결과
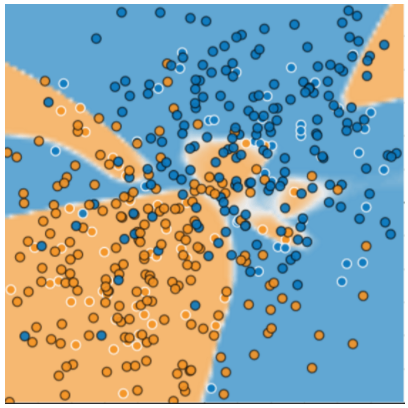
그림 2와 3을 통해 모델이 학습한 데이터에 과적합되었다는 것을 확인할 수 있다. 과적합된 모델은 학습 중에는 loss가 작지만, 새로운 데이터를 예측하는 데는 좋지 않은 성능을 보인다. 모델이 현재 샘플 데이터에 잘 맞는다고 해서 새로운 데이터에도 좋은 예측 성능을 가질 것이라고 어떻게 믿을 수 있는가? 나중에 포스팅 하겠지만, 모델을 필요 이상으로 복잡하게 설계할 때 과적합이 발생한다. 머신러닝의 핵심은 데이터를 가능한 한 간단하게 잘 만드는 것이다. 정말 어려운 문제다…
머신러닝의 목표는 학습한 데이터가 아닌 새로운 실제 데이터를 잘 예측하는 것이다. 하지만 불행히도 모델은 모든 진실을 볼 수 없다. 우리가 학습시키는 학습 데이터 세트만을 볼 수 있을 뿐이다. 그렇다면 모델이 학습시킨 데이터에 대해서 좋은 예측 성능을 보인다고 해서 학습하지 않은 새로운 데이터에서도 좋은 예측 성능을 보일 것이라고 어떻게 믿을 수 있는가?
14세기의 수사이자 철학자인 William of Ockham은 단순함을 사랑했다. 그는 과학자들이 복잡한 공식이나 이론보다 단순한 공식이나 이론을 선호해야 한다고 믿었다. 이 이론은 ‘오컴의 면도날’ 또는 ‘단순성의 원리’등 여러 이름으로 불리며, 이를 머신러닝에 적용하면
The less complex an ML model, the more likely that a good empirical result is not just due to the peculiarities of the sample.
모델이 덜 복잡할수록 좋은 결과가 나올 수 있고, 그것은 꼭 데이터의 특성 때문만은 아닐 가능성이 높다.
말이 좀 어렵지만 쉽게 풀어 말하면 ‘같은 데이터로 복잡한 모델과 단순한 모델을 학습 시킨다면, 복잡한 모델보다 오히려 단순한 모델이 더 좋은 예측 성능을 가질 수 있다’는 것이다.
현대에 와서는, 오컴의 면도날을 ‘통계적 학습 이론’과 ‘전산 학습 이론’의 분야로 공식화 했다. 이러한 필드는 다음과 같은 요인을 기반으로 새로운 데이터로 일반화하기 위한 모델의 능력에 대한 통계적 설명인 일반화 범위를 개발해왔다.
- 모델의 복잡성
- 학습 데이터에 대한 모델의 성능
이론적인 분석은 이상적인 가정 하에서 형식적인 보증을 하지만 실제로는 적용하기 어려울 수 있다.
위에서도 언급했듯이, 머신러닝 모델은 학습하지 않은 새로운 데이터에 대해 좋은 예측을 하는 것이 목표이다. 그러나 데이터 세트를 통하여 모델을 구축하는 경우, 새로운 데이터를 어떻게 얻을 수 있는가? 한 가지 방법은 데이터 세트를 두 개의 하위 집합으로 나누는 것이다.
- training set : 모델을 훈련시키는 데에 사용
- test set : 모델을 테스트하는 데에 사용
테스트 세트를 유용하게 사용하기 위한 조건은 :
- 테스트 세트가 모델을 테스트 하기에 충분히 커야 한다.
- 동일한 테스트 세트를 계속해서 사용하여 부정 행위를 하지 않는다.
The ML fine print
일반화의 세 가지 기본적인 가정이 있다.
- 데이터는 분포에서 독립적이고 동등하게(독립항등분포) 무작위로 만들어져야 한다. 즉, 서로 영향을 미치지 않아야 한다. (변수의 무작위성)
- 분포는 고정적이다. 즉, 데이터 세트 내에서 분포가 변경되지 않는다.
- 동일한 분포의 분할에서 데이터를 뽑아야 한다.
위 가정들을 어길 수 있는 예를 살펴보면 :
- 표시할 광고를 선택하는 모델 : 모델이 부분적으로 사용자가 이전에 본 광고를 기반으로 광고를 선택하는 경우
- 1년 동안의 소비자의 소매 정보가 포함된 데이터 세트 : 사용자의 구매는 계절에 따라 변하므로 고정성이 적용되지 않는다.
따라서, 앞의 세 가지 기본 가정 중 하나라도 위반되는 것을 알게 된다면, 측정의 기준에 주의를 기울여야 한다.
※ 참고
