임베딩 (Embedding)
임베딩(Embedding)은 고차원 벡터를 변환할 수 있도록 하는 저차원 공간이다. 임베딩은 단어를 나타내는 희소 벡터와 같은 대규모 입력값에 대해 머신러닝을 더 쉽게 수행할 수 있게 한다. 이상적으로, 임베딩은 임베딩 공간에서 의미론적으로 유사한 입력값끼리 서로 가깝게 배치하여 입력값의 의미상의 일부를 캡쳐한다. 임베딩은 모델 간에 학습되고 재사용될 수 있다.
협업 필터링의 동기 (Motivation From Collaborative Filtering)
협업 필터링(Collaborative Filtering)은 다른 많은 사용자의 관심사를 기반으로 사용자의 관심사를 예측하는 작업이다. 예를 들어, 영화 추천이라면, 백만 명의 사용자와 이들이 본 영화 목록이 있다고 가정하자. 이를 분석하여 사용자에게 영화를 추천하는 것이다.
이 문제를 해결하려면 서로 유사한 영화들을 판별하는 몇 가지 방법이 필요하다. 유사한 영화들끼리는 가까이 위치하도록 하는 저차원 공간을 만들어 영화를 임베딩함으로써 이 목표를 달성할 수 있다.
임베딩을 학습하는 방법을 설명하기 전에, 먼저 임베딩에 원하는 품질 유형과 임베딩 학습을 위한 교육 데이터를 나타내는 방법을 알아보자.
1차원으로 영화 정렬 (Arrange Movies on a One-Dimensional Number Line)
임베딩에 대한 직관력을 기르기 위해, 아래의 영화들을 1차원으로 유사한 영화들끼리 가깝게 위치하도록 만들어보자.
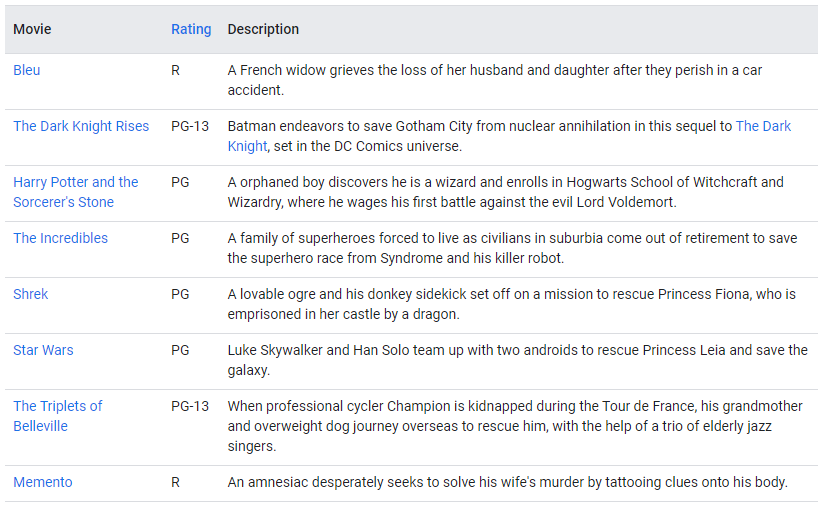

위의 임베딩은 영화를 [어린이 vs. 성인]의 초점에 맞춰줬다. 하지만 영화를 추천할 때, 더 고려해야 할 측면이 아직 더 있기 때문에 한 단계 더 나아가 차원을 추가해 임베딩 해보자.
2차원으로 영화 정렬 (Arrange Movies in a Two-Dimensional Space)
위와 같은 영화 목록을 2차원 공간에 배열한다.
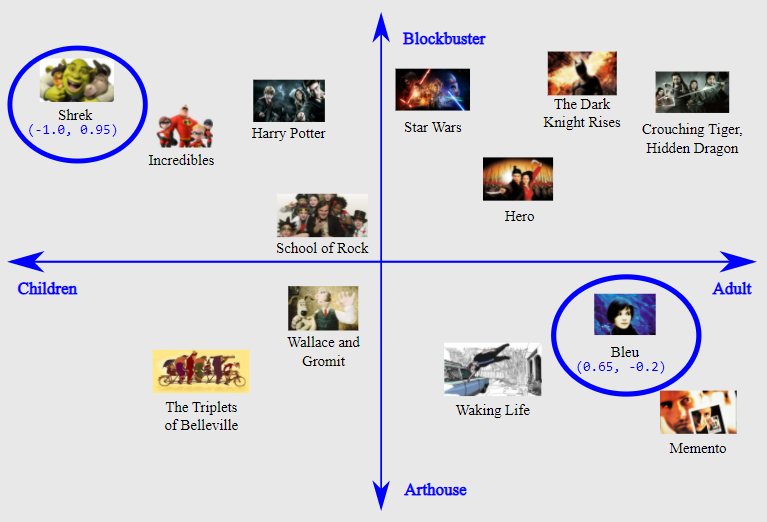
이러한 2차원 임베딩으로 영화가 [어린이 vs. 성인]의 기준뿐만 아니라 [블록버스터 vs. 예술적]의 기준에서도 모두 유사하다면 가까이에 위치하도록(유사한 것으로 추론) 영화 사이의 거리를 정의한다. 물론, 이것들은 고려해야하는 영화의 중요한 특징들 중 두 가지에 불과하다.
좀 더 일반적으로, 위의 작업은 각 단어가 2차원의 좌표 세트로 묘사되는 임베딩 공간(Embedding space)에 영화들을 매핑한 것이다. 예를 들어, 이 공간에서 ‘슈렉’은 (-1.0, 0.95) 위치에 매핑되고, ‘블루’는 (0.65, -0.2) 위치에 매핑된다. 일반적으로, d-차원 임베딩을 학습할 때, 각 데이터는 d개의 실수값으로 표현되며, 각 값은 하나의 차원의 좌표를 나타낸다.
이 예에서 각 차원에 이름을 부여했다. 그러나 임베딩을 학습할 때 개별의 차원은 이름으로 학습되지 않는다. 때때로, 우리는 임베딩을 보고 차원에 의미를 부여할 수도 있고, 할 수 없는 경우도 있다. 종종, 이러한 각 차원은 데이터에 명시되지 않지만 오히려 데이터로부터 추론되는 특징을 나타내기 때문에 잠재 차원이라고 불린다.
궁극적으로, 의미 있는 것은 임베딩 공간에서 데이터 사이의 거리이며, 주어진 차원에 따른 데이터의 값이 아니다.
범주형 입력 데이터 (Categorical Input Data)
범주형 입력 데이터(Categorical Input Data)는 한정된 선택의 집합으로부터 하나 이상의 별개의 항목들을 나타내는 입력 특성을 나타낸다. 예를 들어, 사용자가 본 영화 집합, 문서의 단어 집합, 사람의 직업 등이 될 수 있다.
범주형 데이터는 0이 아닌 요소가 거의 없는 텐서인 희소 텐서(sparse tensor)를 통해 가장 효율적으로 표현된다. 예를 들어, 우리가 영화 추천 모델을 구축한다면, 각 영화에 고유한 ID를 할당하고 사용자가 본 영화의 희소 텐서로 각 사용자를 나타낼 수 있다. 아래의 그림을 보자.

위 행렬의 각 행은 사용자의 영화 시청 기록을 캡쳐하는 예이며, 각 사용자가 모든 영화 중 작은 부분만 시청하기 때문에 희소 텐서로 표현된다. 마지막 행은 영화 아이콘 위에 표시된 지표를 사용하여 희소 텐서 [1, 3, 999999]에 해당한다.
마찬가지로 단어, 문장, 문서를 어휘의 각 단어가 위의 영화 추천 예제와 유사한 역할을 하는 희소 벡터로 나타낼 수 있다.
머신러닝에서 이러한 표현을 사용하기 위해서, 의미적으로 유사한 아이템(영화, 단어)이 벡터 공간에서 유사한 거리를 갖도록 각 희소 벡터를 숫자 벡터로 표현하는 방법이 필요하다. 그러나, 어떻게 숫자로 구성된 벡터로 표현할까?
가장 간단한 방법은 어휘의 모든 단어에 대한 노드 또는 데이터에 나타나는 모든 단어에 대한 노드가 있는 거대한 입력층을 정의하는 것이다. 만약 데이터에 고유한 단어가 500,000개 있는 경우, 길이가 500,000인 벡터로 나타내고 각 단어를 벡터에 할당할 수 있다.
‘horse’를 1247번째에 할당한 다음, 네트워크에 ‘horse’를 공급하려면 1을 1247번째 입력 노드에 목사하고 나머지 모든 노드에 0을 복사해야할 것이다. 이러한 종류의 표현을 하나의 인덱스에만 0이 아닌 값이 있기 때문에 one-hot encoding이라고 부른다.
더 일반적으로 벡터는 더 큰 텍스트 덩어리에 있는 단어의 수를 포함할 수 있다. 이것은 ‘Bag of Words’ 표현으로 알려져 있다. bag of words 벡터에서 500,000개 노드 중 몇 개는 0이 아닌 값을 갖는다.
그러나 0이 아닌 값을 확인하더라도, 단어당 하나의 노드는 매우 희소한 입력 벡터, 즉 벡터의 크기에 비해 0이 아닌 값이 비교적 매우 적은 벡터를 제공한다. 희소 표현은 모델이 효과적으로 학습하는 것을 어렵게 만드는 몇 가지 문제가 있다.
네트워크 크기 (Size of Network)
거대한 입력 벡터는 신경망에 대해 엄청난 수의 가중치를 의미한다. 어휘에 M개의 단어가 있고 네트워크의 첫 번째 층에 N개의 노드가 있다면, 이 계층에 대해 M x N 개의 가중치를 학습해야 한다. 가중치가 많으면 추가 문제를 야기한다.
- 데이터의 양(Amount of data) 모델에 가중치가 많을수록 효과적으로 학습하는 데 더 많은 데이터가 필요하다.
- 연산량(Amount of computation) 가중치가 많을수록 모델을 학습하고 사용하는 데 더 많은 연산이 필요하다. 하드웨어의 기능을 쉽게 초과할 수 있다.
벡터 간의 의미 있는 관계 부족 (Lack of Meaningful Relations Between Vectors)
RGB 채널의 픽셀값을 이미지 분류기에 입력하면, ‘가까운’값에 대해 이야기하는 것이 좋다. 적청색은 의미적으로도 벡터 사이의 기하학적 거리 측면에서도 모두 순수한 파란색에 가깝다. 그러나 ‘horse’에 대한 1247번째에서 1을 갖는 벡터는 ‘television’에 대한 238번째에서 1을 갖는 벡터보다 ‘antelope’에 대한 50,430번째에서 1을 갖는 벡터에 더 가깝지 않다. 즉, 인덱스가 가깝다고해서 의미까지 유사한 것이 아닐 수 있다.
해결책 : 임베딩 (The Solution: Embeddings)
이러한 문제에 대한 해결책은, 큰 희소 벡터를 의미적인 관계를 보존하는 저차원 공간으로 변환하는 임베딩을 사용하는 것이다.
저차원 공간으로의 변환 (Translating to a Lower-Dimensional Space)
고차원 데이터를 저차원 공간으로 매핑하여 희소 입력 데이터의 핵심 문제를 해결할 수 있다.
작은 다차원 공간에서도 의미적으로 유사한 항목을 그룹화하고 유사하지 않은 항목을 멀리 떨어뜨릴 수 있다. 벡터 공간에서의 위치(거리 및 방향)는 의미론적인 것들을 좋은 임베딩으로 인코딩할 수 있다. 예를 들어, 아래의 시각화 자료는 실제로 국가와 수도 같의 관계와 같은 의미론적 관계를 기하학적으로 표현한 것이다.
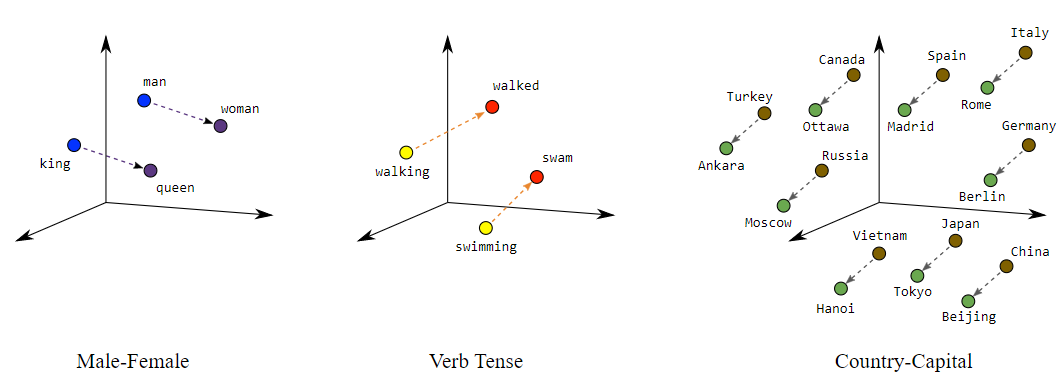
이러한 종류의 의미 있는 공간은 머신러닝 시스템이 학습할 때, 도움이 될 수 있는 패턴을 감지할 수 있는 기회를 제공한다.
네트워크 축소 (Shrinking the network)
풍부한 의미 관계를 인코딩할 수 있는 충분한 차원을 원하지만, 또한 시스템을 더 빠르게 학습할 수 있는 충분한 임베딩 공간도 필요하다. 유용한 임베딩은 수백 차원일 수도 있다. 이는 자연어 처리에 대한 어휘의 크기보다 몇 자릿수는 더 작을 것이다.
룩업 테이블로서 임베딩 (Embeddings as lookup tables)
임베딩은 각 열이 어휘의 항목에 해당하는 벡터인 행렬이다. 단일 어휘 항목에 대한 밀집 벡터를 얻으려면 그 항목에 해당하는 열을 검색한다.
그러나, 어떻게 희소 ‘bag of words’ 벡터를 변환하는가? 여러 어휘 항목(문장, 문단의 모든 단어)을 나타내는 희소 벡터의 밀집 백터를 얻으려면, 각 개별 항목의 임베딩을 검색한 다음 그것들을 추가한다.
희소 벡터가 어휘 항목의 수를 포함하고 있다면, 합계에 추가하기 전에 각 임베딩에 해당하는 항목의 수를 곱한다.
행렬 곱으로 임베딩 검색 (Embedding lookup as matrix multiplication)
방금 설명한 조회, 곱셈, 추가 절차는 행렬 곱과 동일하다. l x n 희소 표현 S와 n x m 임베딩 테이블 E가 주어지면, 행렬 곱 SE는 l x m 밀집 벡터가 된다.
그러나 처음에 E를 어떻게 얻는가?
임베딩 얻기 (Obtaining Embeddings)
표준 차원 축소 기법 (Standard Dimensionality Reduction Techniques)
저차원 공간에서 고차원 공간의 중요한 구조를 포착하기 위한 수학적 기술들이 많이 존재한다. 이론적으로, 이러한 기술들 중 하나를 사용하여 머신러닝 시스템을 위한 임베딩을 생성할 수 있다.
예를 들어, 주성분 분석(PCA:Principal component analysis)은 단어 임베딩을 만드는 데 사용된다. ‘bag of words’ 벡터와 같은 인스턴스가 주어지면, PCA는 단일 차원으로 축소될 수 있는 상관 관계가 높은 차원을 찾기위해 시도한다.
Word2Vec
‘Word2Vec’은 단어 임베딩을 학습하기 위해 Google에서 개발한 알고리즘이다. Word2Vec은 의미적으로 유사한 단어를 기하학적으로 가까운 임베딩 벡터에 매핑하기 위해 분포 가설(distributional hypothesis)에 의존한다.
분포 가설은 종종 동일한 인접 단어를 갖는 단어가 의미적으로 유사한 경향이 있다고 말한다. ‘dog’와 ‘cat’은 모두 ‘vet’이라는 단어와 가깝게 나타나는 경우가 많으며 이 사실은 의미론적 유사성을 반영한다. 언어학자 존 퍼스(John Firth)가 1957년 말했들이 “당신이 그것이 유지하는 회사에 의해 단어를 알게 될 것입니다.”
Word2Vec은 실제로 동시 발생하는 단어 그룹을 무작위로 그룹화된 단어와 구별하도록 신경망을 학습함으로써 맥락과 관련된 정보를 활용한다. 입력 계층은 하나 이상의 문맥의 단어와 함께 타켓 단어의 희소 표현을 사용한다. 이 입력은 하나의 더 작은 은닉층에 연결된다.
알고리즘의 한 버전에서, 시스템은 타켓 단어에 대해 임의의 노이즈를 대체하여 negative label를 만든다. 예를 들어, ‘비행기가 날다’라는 positive label가 주어지면, 시스템은 ‘조깅’으로 바꾸어 ‘조깅이 날다’라는 negative label를 생성한다.
다른 버전은 실제 실제 타켓 단어를 무작위로 선택한 문맥의 단어와 짝을 만들어 negative label를 만든다. 예를 들어, positive label (the, plane), (flies, plane) 및 negative label (compiled, plane), (who, plane)를 만들어 실제로 텍스트에서 함께 등장하는 쌍을 식별하는 방법을 배운다.
그러나 어떤 버전이라도 분류기를 만드는 것이 진정한 목표가 아니다. 모델의 학습이 끝난 후에는, 임베딩을 가지고 있을 것이다. 입력층과 은닉층을 연결하는 가중치를 사용하여 희소 표현을 더 작은 벡터에 매핑할 수 있다. 이 임베딩은 다른 분류기에서 재사용할 수 있다.
더 자세한 정보는 tutorial on tensorflow.org를 참고하자.
더 큰 모델의 일부로서 임베딩 학습 (Training an Embedding as Part of a Larger Model)
신경망의 일부로서 임베딩을 학습할 수 있다. 이 접근 방식은 특정 시스템에 대해 잘 맞춤화된 임베딩을 얻을 수 있지만, 임베딩을 별도로 학습하는 것보다 더 오랜 시간이 걸릴 수 있다.
일반적으로 희소 데이터(또는 임베딩하고 싶은 밀집 데이터)를 가지고 있을 때, 크기가 d인 숨겨진 단위의 특별한 타입인 임베딩 단위를 만들 수 있다. 이 임베딩층은 다른 특성들 및 은닉층과 결합할 수 있다. 어떤 DNN에서와 마찬가지로, 최종층은 최적화 되는 loss가 된다. 예를 들어, 다른 사용자들의 관심사로부터 사용자의 관심사를 예측하는 것이 목표인 협업 필터링을 수행한다고 하자.
이것을 positive label로서 무작위로 사용자가 본 영화들을 따로 설정한 다음 softmax loss를 최적화하여 지도 학습 문제로 모델링할 수 있다.
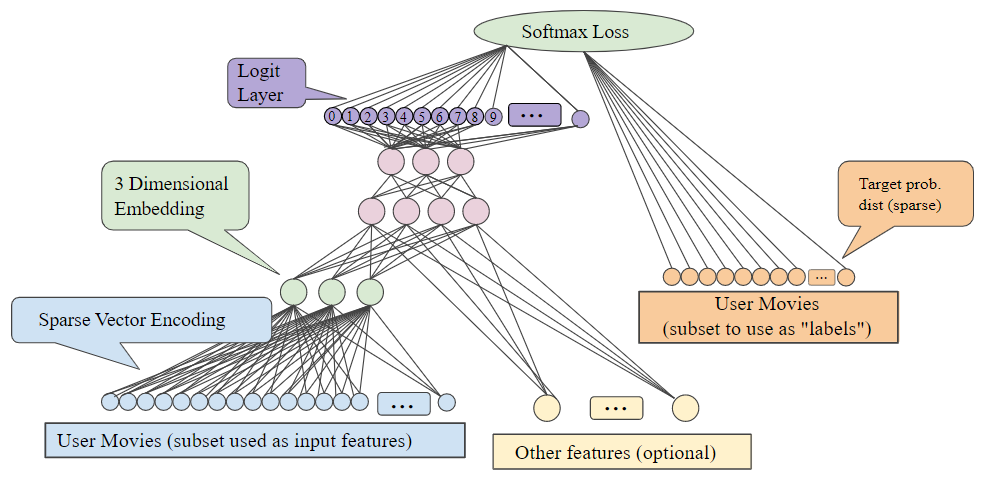
또 다른 예로, 만약 주택 가격을 예측하기 위해 DNN의 일부로서 부동산 광고의 단어에 대한 임베딩층을 만들고 싶다고 한다면, label로서 알려진 training data의 주택 판매 가격을 사용하여 L2 loss를 최적화한다.
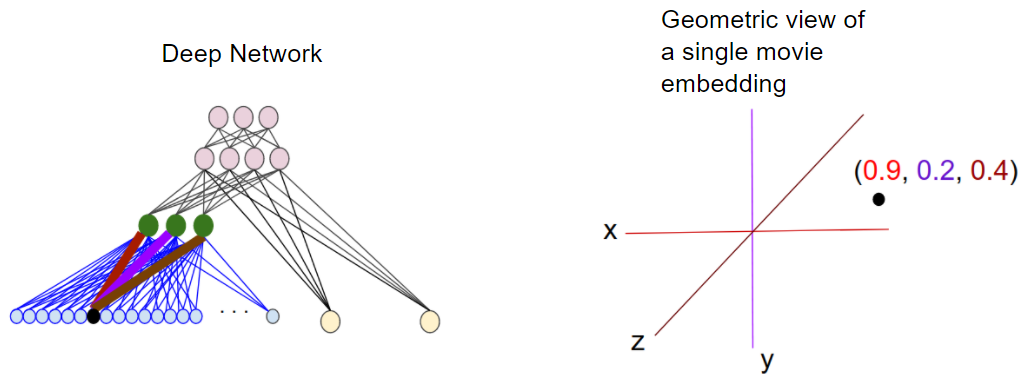
d차원 임베딩을 학습할 때, 각 항목은 d차원 공간의 한 지점에 매핑되어 이 공간에서 유사한 항목은 근처에 있다. 아래의 그림은 임베딩층에서 학습된 가중치와 기하학적인 관점 사이의 관계를 설명하는 데 도움이 된다. 입력 노드와 d차원 임베딩층의 노드 사이의 edge weights는 각 차원축의 좌표 값에 해당한다.
※ 참고
Google Developer - Motivation From Collaborative Filtering
Google Developer - Categorical Input Data
Google Developer - Translating to a Lower-Dimensional Space
Google Developer - Obtaining Embeddings
