Kyoungtae Min

진화하는 엔지니어가 되기 위한, 공부 내용 정리 및 기록

5 분 소요

Softmax Model

행렬 분해를 사용하여 임베딩을 학습하는 방법을 공부했다. 행렬 분해의 몇 가지 제한 사항은 다음과 같다.

  • 부수적 특성(query, ‘items’ 이외의 특성) 사용의 어려움. 결과적으로 모델은 학습 세트에 있는 사용자 또는 items으로만 쿼리할 수 있다.
  • 추천의 연관성. 인기 있는 items는 특히 내적으로 유사도를 측정할 때 모든 사람에게 추천되는 경향이 있다. 그러나, 특정 사용자의 관심사를 포착하는 것이 더 좋다.

심층 신경망(DNN: Deep Neural Network) 모델은 이러한 행렬 분해의 한계를 해결할 수 있다. DNN은 네트워크 입력층의 유연성으로 query 특성과 items 특성을 쉽게 통합할 수 있으며, 사용자의 특정 관심사를 포작하고 추천의 연관성을 향상시키는 데 도움이 될 수 있다.

추천을 위한 Softmax DNN (Softmax DNN for Recommendation)

가능한 DNN 모델 중 하나는, 문제를 다중 클래스 예측 문제로 취급하는 softmax 이다.

  • 입력은 사용자 query이다.
  • 출력은 각 item과 상호 작용할 확률을 나타내는 코퍼스 내의 items의 수와 크기가 동일한 확률 벡터이다. 예를 들면, YouTube 영상을 클릭하거나 시청할 확률이다.

입력 (Input)

DNN에 입력할 때, 다음이 포함될 수 있다.

  • 밀집 특성 (dense feature, 예: 시청 시간 및 마지막 시청 이후 시간)
  • 희소 특성 (sparse feature, 예: 시청 기록 및 국가)

행렬 분해 접급 방식과 달리, 나이 또는 국가와 같은 부수적 특성을 추가할 수 있다. 입력 벡터를 x로 정의하겠다.


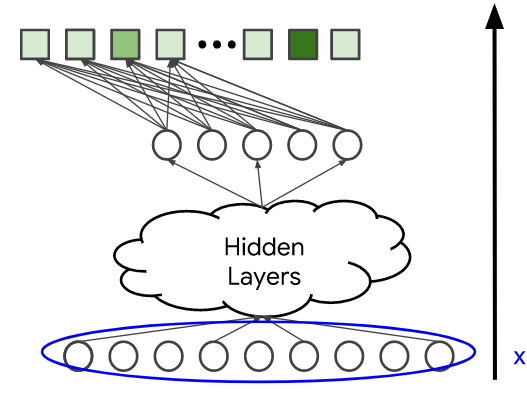
모델 구성 (Model Architecture)

모델 구성은 모델의 복잡도와 표현도를 결정한다. 은닉층과 비선형 활성화 함수(예: ReLU)를 추가함으로써, 모델은 데이터에서 더 복잡한 관계를 포작할 수 있다.
그러나 매개변수의 수를 늘리는 것은 일반적으로 모델을 학습시키기가 더 어렵고 제공하는 데 비용이 더 많이 든다. 마지막 은닉층의 출력을 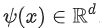로 표시한다.


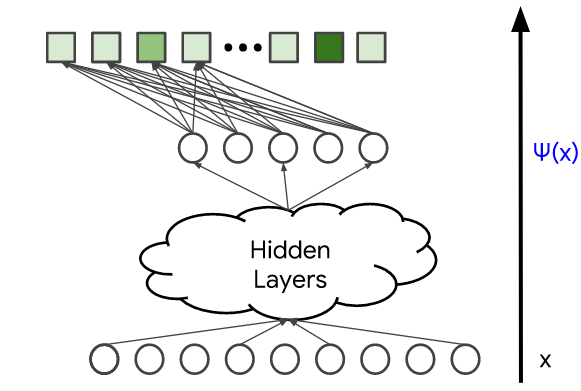
Softmax 출력: 예측 확률 분포 (Softmax Output: Predicted Probability Distribution)

모델은 마지막 레이어의 출력인 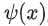를 softmax 레이어를 통해 확률 분포 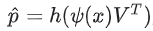에 매핑한다.

  • h : 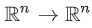은 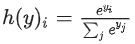로 주어진 softmax 함수이다.
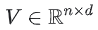  • 은 softmax 레이어의 가중치 행렬이다.

softmax 레이어는 점수 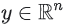(logits 이라고도 함)의 벡터를 확률 분포에 매핑한다.


‘softmax’라는 이름은 말장난이다. ‘hardmax’는 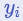가 가장 큰 item에 확률 1을 할당한다. 대조적으로 softmax는 모든 items에 0이 아닌 확률을 할당하여 점수가 더 높은 item에 더 높은 확률을 부여한다. 점수가 조정될 때, softmax 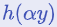는 극한 에서 hardmax로 수렴된다.

손실 함수 (Loss Fuction)

마지막으로 다음을 비교하는 손실 함수를 정의한다.

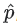  • : softmax 레이어의 출력 (확률 분포)
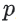  • : 사용자가 상호작용한(예: 사용자가 클릭하거나 본 영상) items를 나타내는 실측값이다. 이것은 정규화된 multi-hot 분포(확률 벡터)로 나타낼 수 있다.

예를 들어, 두 개의 확률 분포를 비교하기 위해 cross-entropy loss를 사용할 수 있다.


Softmax 임베딩 (Softmax Embedding)

item j의 확률은 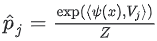이다. 여기서 Z는 j에 종속되지 않는 정규화 상수이다. 즉, 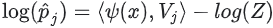이므로 item j의 로그 확률은(추가 상수까지) query 및 item 임베딩으로 해설될 수 있는 두 d-차원의 내적이다.

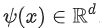  • 는 마지막 은닉층의 출력이다. 이를 query x의 임베딩이라고 한다.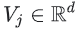
  • 는 마지막 은닉층을 출력 j에 연결하는 가중치 벡터이다. 이를 item j의 임베딩이라고 한다.

log는 증가 함수이므로, 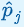확률이 가장 높은 item j는 내적 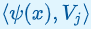가 가장 높은 item이다. 따라서 내적은 이 임베딩 공간에서 유사도 측정 척도로 해석될 수 있다.


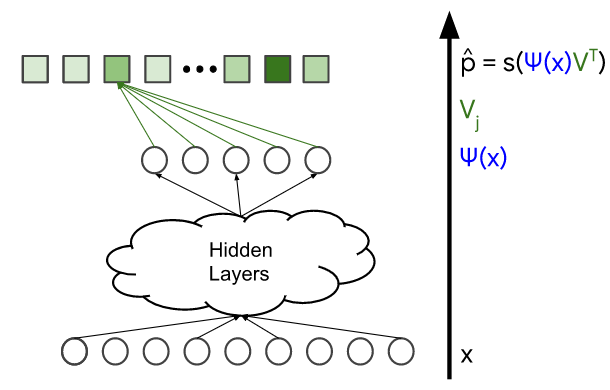
DNN과 행렬 분해 (DNN and Matrix Factorization)

softmax 모델과 행렬 분해 모델 모두, 시스템은 item j 당 하나의 임베딩 벡터 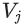를 학습힌다. 행렬 분해에서 item 임베딩 행렬이라고 부르는 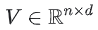은 softmax 레이어의 가중치 행렬이다.

그러나 query 임베딩은 다르다. query i 당 하나의 임베딩 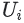를 학습하는 대신, 시스템은 query 특성 x에서 임베딩 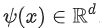로의 매핑을 학습한다. 따라서 이 DNN 모델은 query 측을 비선형 함수 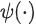로 대체하는 행렬 분해의 일반화로 생각할 수 있다.

Item 특성을 사용할 수 있는가? (Can You Use Item Features?)

그렇다면 item 측에도 같은 아이디어를 적용할 수 있는가? 즉, item 당 하나의 임베딩을 학습하는 대신, 모델이 item 특성을 임베딩에 매핑하는 비선형 함수를 학습할 수 있는가? 그렇다. 실행하기 위해서는 두 개의 신경망으로 구성된 two-tower 신경망을 사용한다.

  • 하나의 신경망은 query 특성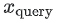 을, query 임베딩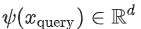 에 매핑한다.
  • 하나의 신경망은 item 특성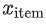 을, item 임베딩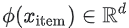 에매핑한다.

모델의 출력은 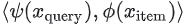의 내적으로 정의할 수 있다. 이것은 더 이상 softmax 모델이 아니다. 새 모델은 각 query 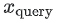에 대한 확률 벡터 대신 쌍 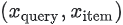당 하나의 값을 예측한다.

Softmax Training

시스템의 학습 데이터를 자세히 살펴보자.

학습 데이터 (Training Data)

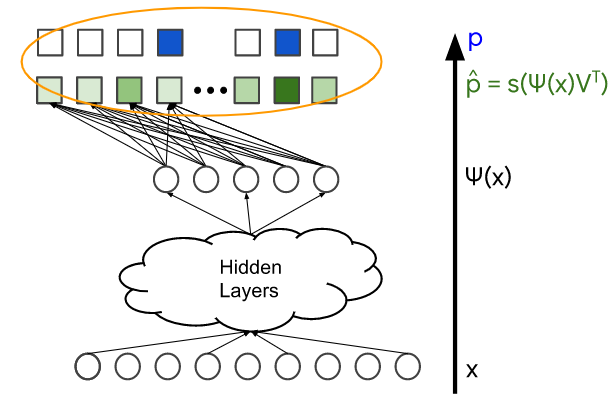
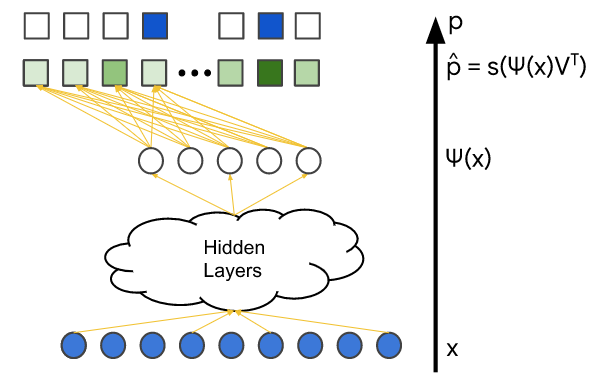
softmax 학습 데이터는 query 특성 x와 사용자가 상호 작용한 items의 벡터(확률 분포 p로 표현)로 구성된다. 아래의 그림에서 파란색으로 표시되어 있다. 모델의 변수는 다른 레이어들에서 가중치이다. 이는 아래의 그림에서 주황색으로 표시되어 있다. 모델은 일반적으로 확률적 경사 하강법의 변형을 사용하여 학습힌다.


Negative Sampling

손실 함수(loss function)는 두 개의 확률 벡터 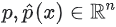(각각 모델의 정답과 출력)을 비교하므로, 코퍼스의 사이즈 n이 너무 크면 단일 query x에 대한 손실의 기울기를 계산하는 것은 엄청나게 비용이 많이 들 수 있다.

positive items(실측값 벡터에서 활성화된 items)에 대해서만 기울기를 계산하도록 시스템을 설정할 수 있다. 그러나 시스템이 positive 쌍에 대해서만 학습하는 경우, 모델이 접히는 folding 문제가 발생할 수 있다.

Folding


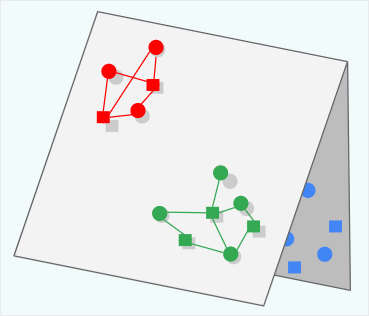
위의 그림에서 각 색상이 queries 및 items의 다른 카테고리를 나타낸다고 가정하자. 각 query(정사각형)는 대부분 동일한 색상의 items(원)과만 상호작용한다. 예를 들어, YouTube에서 각 카테고리를 다른 언어라고 가정하자. 일반적인 사용자는 주로 하나의 특정 언어로 된 영상과 상호작용한다.

모델은 주어진 색상의 query/items 임베딩을 서로에 대해 해당 색상 내에서 유사도를 정확하게 포착하여 배치하는 방법을 학습할 수 있다. 그러나 우연히 다른 색상의 임베딩이 같은 임베딩 공간의 같은 영역에 포함될 수 있다. folding이라고 하는 이 현상은 잘못된 추천으로 이어질 수 있다. query 시간에 모델이 다른 그룹의 item에 대해 높은 점수를 매겨 잘못 예측할 수 있다.

Negative examples은 주어진 query와 ‘관련 없음’으로 label이 지정된 item이다. 학습 중에 모델에 negative examples를 보여주면 모델이 서로 다른 그룹의 임베딩을 서로 밀어내야 한다는 것을 가르친다.

모든 items를 사용하여 gradient를 계산하거나(비용이 너무 많이 들 수 있음) positive items만 사용하는(folding 문제가 발생할 수 있음) 대신, Negative sampling을 사용할 수 있다.

보다 정확하게 얘기하자면 다음의 items를 사용하여 대략적인 gradient를 계산한다.

  • 모든 positive items (target label이 나타나는 항목)
  • negative items의 samples (1 부터 n까지 중 j에 해당하는 항목)

negative sampling에는 다양한 전략들이 있다.

  • 균일하게 샘플링할 수 있다.
  • 더 높은 점수 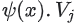를 가진 items j에 더 높은 확률을 부여할 수 있다. 직관적으로 이것은 gradient에 가장 많이 기여한다. 이를 ‘hard negative’라고도 한다.

행렬 분해 vs. Softmax (Matrix Factorization Vs. Softmax)

DNN 모델은 행렬 분해의 많은 제한 사항을 해결하지만, 일반적으로 학습 및 query 비용이 더 많이 든다. 아래의 표는 두 모델 간의 몇 가지 중요한 차이점을 요약한 것이다.


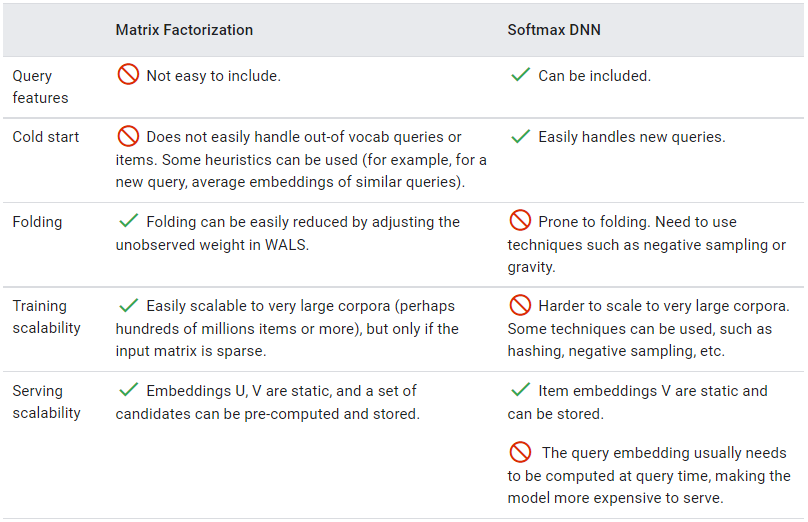
요약 :

  • 행렬 분해는 일반적으로 큰 코퍼스에 더 나은 선택이다. 확장하기 쉽고, query 비용이 저렴하며 folding 문제가 적게 일어난다.
  • DNN 모델은 개인화된 선호도를 더 잘 포착할 수 있다. 하지만 학습하기 어렵고 query 비용이 더 많이 든다. DNN 모델은 연관성을 더 잘 포착하기 위해 더 많은 기능을 사용할 수 있기 때문에, scoring을 위해 행렬 분해보다 선호된다. 또한 연관성이 있다고 가정되는 사전 필터링된 후보 집합의 순위를 지정하는 데 주로 관심을 갖기 때문에, 일반적으로 DNN 모델에 folding 문제가 발생하더라도 허용된다.


※ 참고

Google Developer - Deep Neural Network Models
Google Developer - Softmax Training

참고