추천 시스템: 협업 필터링 (Collaborative filtering)

6 분 소요

컨텐츠 기반 필터링(content-based filtering)의 일부 제한 사항을 해결하기 위해, 협업 필터링(collaborative filtering)은 사용자와 items 간의 유사성을 동시에 사용하여 추천한다. 이는 우연히 발견되는 추천이 가능하도록 한다. 즉, 협업 필터링 모델은 사용자 A와 유사한 사용자 B의 관심사를 기반으로 A에게 items를 추천할 수 있다. 또한 특성을 수공으로 엔지니어링하지 않고 임베딩을 자동으로 학습할 수 있다.

예: 영화 추천 (A Movie Recommendation Example)

training data가 다음과 같은 피드백 행렬로 구성된 영화 추천 시스템을 구축한다고 가정하자.

각 행은 사용자를 나타낸다.
각 열은 item(영화)을 나타낸다.

영화에 대한 피드백은 다음 두 가지 범주 중 하나로 분류된다.

명시적 - 사용자는 평점를 매겨 특정 영화가 얼마나 좋았는지 명시한다.
암시적 - 사용자가 특정 영화를 보는 경우, 시스템은 사용자가 그 영화에 흥미를 갖는다고 추론한다.

여기서는 간단하게하기 위해, 피트백 행렬이 이진법으로 구성되었다고 가정한다. 즉, 값이 1이면 영화에 대한 관심을 나타낸다.

사용자가 홈페이지를 방문하면, 시스템은 다음 두 가지를 기반으로 영화를 추천해야 한다.

사용자가 과거에 좋아했던 영화와의 유사도
추천 받을 사용자와 유사한 사용자가 좋아한 영화

예를 돕기 위해, 다음 표에 설명된 영화의 일부 특성을 직접 엔지니어링 해보자.

1차원 임베딩 (1D Embedding)

영화가 어린이용인지(음수 값) 성인용인지(양수 값)를 설명하는 [-1, 1]에, 각 영화에 해당하는 스칼라 값을 할당한다고 가정하자. 또한 어린이용에 관심을 갖는지(-1에 가까움) 성인용에 관심을 갖는지(+1에 가까움)를 설명하는 [-1, 1]에, 각 사용자에 해당하는 스칼라 값을 할당한다고 가정하자. 영화 임베딩과 사용자 임베딩의 곱은 사용자가 좋아할 것으로 예상되는 영화에 대해 더 높아야 된다.(1에 가까움)

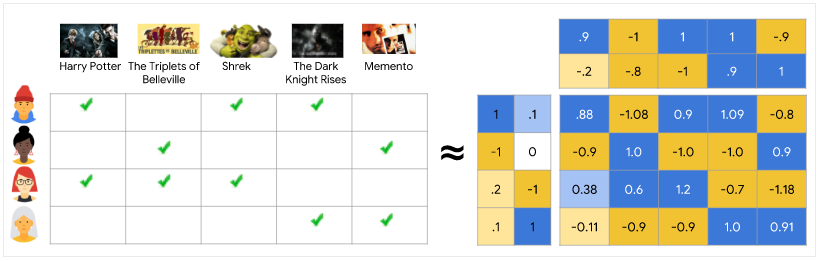
아래의 다이어그램에서 각 체크 표시는 특정 사용자가 시청한 영화를 식별한다. 세 번째 및 네 번째 사용자는 이 특성에 의해 잘 설명되는 선호도를 가지고 있다. 세 번째 사용자는 어린이용 영화를 선호하고, 네 번째 사용자는 성인용 영화를 선호한다. 그러나 첫 번째 사용자와 두 번째 사용자의 선호도는 이 단일 특성으로 잘 설명되지 않는다.

2차원 임베딩 (2D Embedding)

하나의 특성은 모든 사용자의 선호도를 설명하기에는 충분하지 않다. 이 문제를 극복하기 위해, 각 영화가 블록버스터 또는 예술적 중 어디에 가까운지의 정도를 나타내는 두 번째 특성을 추가하겠다. 두 번째 특성을 사용하여 이제 2차원 임베딩으로 각 영화를 나타낼 수 있다.

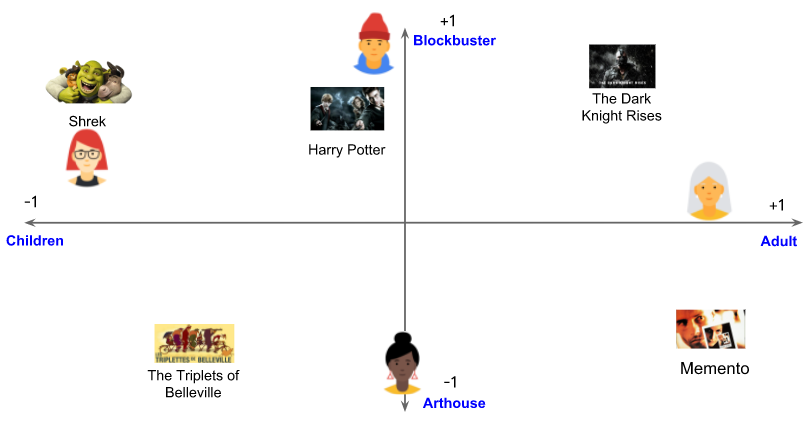
피드백 행렬을 가장 잘 설명하기 위해 사용자를 동일한 임베딩 공간에 다시 배치하자. 각 (사용자, item) 쌍에 대해 사용자 임베딩과 item 임베딩의 내적이 사용자가 그 영화를 시청할 때 1에 가깝고, 그렇지 않으면 0에 가깝기를 원한다.

동일한 임베딩 공간에 item과 사용자를 모두 표시했다. 이것이 놀라운 것처럼 보일 수 있다. 어쨌든 사용자와 items는 서로 다른 두 독립체이다. 그러나 임베딩 공간을 items와 사용자 모두에게 공통적인 추상적인 표현으로 생각할 수 있다. 여기서 유시도 측정을 사용하여 유사도 또는 관련성를 측정할 수 있다.

이 예시에서 임베딩을 직접 엔지니어링 해보았다. 실제로는 임베딩을 자동적으로 학습될 수 있으며 이는 협업 필터링 모델의 힘이다.

이 접근 방식의 협력적 특성은 모델이 임베딩을 학습할 때 명확히 나타난다. 영화에 대한 임베딩 벡터가 고정되어 있다고 가정하자. 그런 다음 모델은 사용자의 선호도를 가장 잘 설명할 수 있도록 임베딩 벡터를 학습할 수 있다. 결과적으로 유사한 선호도를 가진 사용자의 임베딩은 서로 밀접하게 연관된다. 유사하게, 사용자에 대한 임베딩이 고정되면 피드백 행렬을 가장 잘 설명하기 위해 영화 임베딩을 학습할 수 있다. 결과적으로 유사한 사용자가 좋아하는 영화의 임베딩은 임베딩 공간에서 가깝게 위치한다.

행렬 분해 (Matrix Factorization)

행렬 분해(matrix factorization)은 간단한 임베딩 모델이다. 사용자 또는 query의 수가 m이고 items의 수가 n인 피드백 행렬 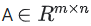이 주어지면, 모델은 다음을 학습한다.

사용자 임베딩 행렬 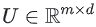(여기서 행 i는 사용자 i에 대한 임베딩이다.)
item 임베딩 행렬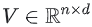 (여기서 행 j는 item j에 대한 임베딩이다.)

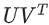가 피드백 행렬 A의 좋은 근사값이 되도록 임베딩이 학습된다. 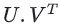의 (i, j) 항목은 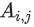에 가깝고자 하는 사용자 i와 item j의 임베딩의 내적 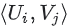이다.

행렬 분해는 일반적으로 전체 행렬을 학습하는 것보다 더 간결한 표현을 제공한다. 전체 행렬에는 O(nm)개의 항목이 있는 반면, 임베딩 행렬 U, V에는 O((n + m)d)개의 항목이 있다. 여기서 임베딩 차원 d는 일반적으로 m, n보다 훨씬 작다. 결과적으로 행렬 분해는 관측값이 저차원 부분 공간에 가깝다고 가정하여 데이터에서 잠재 구조를 찾는다. 앞의 예에서 n, m 및 d의 값은 너무 낮아 이점이 무시될 수 있다. 그러나 실제 추천 시스템에서 행렬 분해는 전체 행렬을 학습하는 것보다 훨씬 더 간결할 수 있다.

목적 함수 고르기 (Choosing the Objective Function)

직관적인 목적 함수(objective function) 중 하나는 거리 제곱이다. 이를 실행하려면 관찰된 모든 항목의 쌍에 대한 오차 제곱 합을 최소화한다.

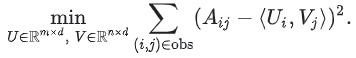
이 목적 함수에서는 관찰된 쌍 (i, j), 즉 피드백 행렬의 0이 아닌 값에 대해서만 합을 계산한다. 그러나 하나의 값만 합산하는 것은 좋은 생각이 아니다. 모든 값으로 구성된 행렬은 손실이 최소화되고 효과적인 추천을 만들 수 없고 일반화되지 않는 모델을 생성한다.

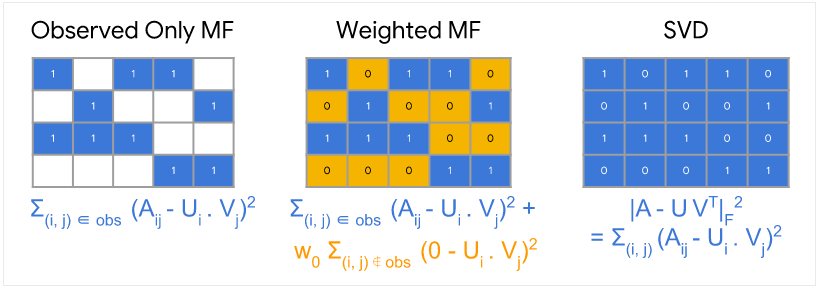
관찰되지 않은 값을 0으로 처리하고 행렬의 모든 항목을 합산할 수 있다. 이것은 A와 그 근사치 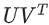사이의 프로베니우스 거리(Frobenius)의 제곱을 최소화하는 것에 해당한다.

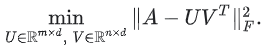
이 2차 문제는 행렬의 SVD(Singular Value Decomposition)를 통해 해결할 수 있다. 그러나 실제 응용 프로그램에서 행렬 A가 매우 희소할 수 있기 때문에 SVD도 훌륭한 솔루션이 아니다. 예를 들어, 특정 사용자가 본 모든 영상과 YouTube의 모든 영상을 비교한다고 생각해보자. 모델의 입력 행렬 근사치에 해당하는 솔루션 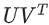는 0에 가까우므로 일반화 성능이 저하될 수 있다.

대조적으로, Weighted Matrix Factorization은 목적을 다음 두 개의 합으로 분해한다.

관찰된 항목에 대한 합계
관찰되지 않은 항목에 대한 합 (0으로 처리됨)

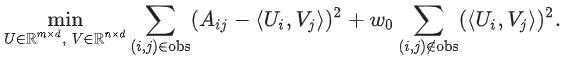
여기서 w0은 목적이 어느 하나에 의해 지배되지 않도록 두 항에 가중치를 부여하는 하이퍼파라미터이다.

실제 응용 프로그램에서는 관찰된 쌍에 신중하게 가중치를 부여해야 한다. 예를 들어, 빈번한 items(예: 매우 인기 있는 영상) 또는 빈번한 query(예: 헤비 유저)가 목적 함수를 지배할 수 있다. items의 빈도를 설명하기 위해 학습 데이터에 가중치를 주어 이 효과를 수정할 수 있다. 즉, 목적 함수를 다음과 같이 바꿀 수 있다.

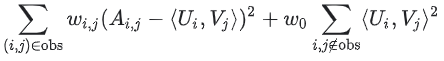
여기서 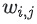은 query인 i와 items인 j의 빈도의 함수이다.

목적 함수 최소화 (Minimizing the Objective Function)

목적 함수를 최소화하는 일반적인 알고리즘은 다음과 같다.

확률적 경사 하강법(SGD: Stochastic gradient descent)은 손실 함수를 최소화하는 일반적인 방법이다.
WALS(Weighted Alternating Least Squares)는 특정 목적에 특화되어 있다.
- 목적은 두 행렬 U, V 각각 2차이다. (그러나 문제는 모두 볼록하지 않다.) WALS는 임베딩을 무작위로 초기화한 다음, 다음을 번갈아 가며 동작한다.
  - U를 고정하고 V를 해결한다.
  - V를 고정하고 U를 해결한다.

각 단계는 (선형 시스템의 솔루션을 통해) 정확하게 풀릴 수 있고 분산될 수 있다. 이 기술은 각 단계가 손실을 줄이는 것이 보장되기 때문에 수렴이 보장된다.

확률적 경사 하강법(SGD) vs. WALS

SGD와 WALS에는 장점과 단점이 있다. 아래 정보를 검토하여 비교 방법을 확인하자.

SGD

장점 : 매우 유연함. 다른 손실 함수를 사용할 수 있다.

장점 : 병렬화할 수 있다.

단점 : 느림. 수렴이 빠르지 않다.

단점 : 관잘되지 않은 항목을 처리하기가 어렵다. (negative sampling 또는 gravity를 사용해야 한다.)

WALS

장점 : 병렬화할 수 있다.

장점 : SGD보다 빠르게 수렴한다.

장점 : 관찰되지 않은 항목을 더 쉽게 처리할 수 있다.

단점 : 손실 제곱에만 의존한다.

장점 & 단점 (Advantages & Disadvantages)

장점 (Advantages)

도메인 지식이 필요하지 않음
- 임베딩이 자동으로 학습되기 때문에 도메인 지식이 필요하지 않다.
뜻밖의 발견 (Serendipity)
- 이 모델은 사용자가 새로운 관심사를 찾는 데 도움이 될 수 있다. 별도로 ML 시스템은 사용자가 특정 items에 관심이 있다는 것을 모를 수 있다. 하지만 이 사용자와 유사한 다른 사용자가 해당 items에 관심이 있기 때문에 모델은 추천할 수 있다.
훌륭한 출발점
- 어느 정도까지는 시스템이 행렬 분해 모델을 학습하기 위해 오직 피드백 행렬만을 필요로한다. 특히, 시스템은 상황에 맞는 특성을 필요로 하지 않는다. 실제로 이것은 여러 후보 생성기 중 하나로 사용될 수 있다.

단점 (Disadvantages)

새로운 items를 취급할 수 없음
- 주어진 (사용자, item) 쌍에 대한 모델의 예측은 해당 임베딩의 내적이다. 따라서 학습 중에 item이 표시되지 않으면 시스템에서 해당 item에 대한 임베딩을 생성할 수 없으며 이 item으로 모델을 query할 수 없다.
- WALS의 추청 : 학습에 볼 수 없는 새 item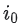 가 주어지면 시스템이 사용자와 조금의 상호 작용이 있는 경우, 시스템은 전체 모델을 다시 훈련할 필요 없이 이 item에 대한 임베딩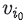 을 쉽게 계산할 수 있다. 시스템은 단순히 다음 방정식을 풀면 된다.
위 방정식은 WALS의 한 번의 반복에 해당한다. 사용자 임베딩은 고정된 상태로, 시스템은 item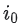 의 임베딩을 해결한다.
- 새로운 items의 임베딩을 생성하는 휴리스틱(Heuristics) : 시스템에 상호 작용이 없는 경우, 시스템은 동일한 카테고리, 동일한 업로더(예: YouTube) 등의 items의 임베딩을 평균화하여 임베딩을 근사화할 수 있다.
query/item에 대한 부수적 특성을 포함하기 어려움
- 부수적 특성은 query 또는 item의 ID를 넘어선 모든 특성이다. 영화 추천의 경우, 부수적 특성에는 국가 또는 연령 등이 포함될 수 있다. 사용 가능한 부수적 특성을 포함하면 모델의 품질이 향상된다. WALS에 부수적 특성을 포함하는 것은 쉽지 않을 수 있지만, WALS를 일반화하면 가능하다.
- WLAS를 일반화하기 위해서는, 블록 행렬 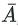를 정의하여 특성으로 입력 행렬을 확장한다.
  - 블록 (0, 0)은 원래 피드백 행렬 A 이다.
  - 블록 (0, 1)은 사용자 특성의 multi-hot encoding 이다.
  - 블록 (1, 0)은 item 특성의 multi-hot encoding 이다.
  - 블록 (1, 1)은 일반적으로 비어있다. 행렬 분해를 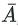에 적용하면 시스템은 사용자 및 item 임베딩 외에도 부수적 특성에 대한 임베딩을 학습힌다.