분류 (Classification)
분류 작업에 로지스틱 회귀를 사용하는 방법과 분류 모델의 효율성을 평가하는 방법을 알아보자.
임계값 (Threshold)
로지스틱 회귀는 확률을 반환한다. 반환된 확률을 ‘있는 그대로’ 사용하거나(에: 사용자가 광고를 클릭할 확률=0.00023) 반환된 확률을 이진값으로 변환하여 사용할 수 있다.(예: 이 메일은 스팸이다)
특정 메일에 대해 0.9995를 반환하는 로지스틱 회귀 모델은 이 메일이 스팸일 가능성이 매우 높다고 예측한다. 반대로, 다른 하나의 메일에 대해 0.0003의 예측값을 반환했다면 이 메일은 스팸이 아닐 가능성이 매우 높다. 그러나, 예측 확률이 0.6인 메일에 대해서는 어떤가? 로지스틱 회귀 모델의 예측값을 이진 범주로 매핑하려면 분류 임계값(Threshold 또는 결정 임계값(Decision Threshold)이라고도 함)을 정의해야 한다. 이 임계값을 초과하는 값은 ‘스팸’을 나타내고, 이하의 값은 ‘스팸 아님’을 의미한다. 분류 임계값은 항상 0.5이어야 하지만, 문제에 따라 달라지므로 조정해야 하는 값이라고 이해하고 있는 것이 더 좋을 것이다.
로지스틱 회귀에 대한 임계값의 ‘조정’은 learning rate와 같은 하이퍼파라미터 조정과는 좀 다르다. 임계값을 얼마로 설정하는지의 선택에 따라 얼마나 고통받을지 가늠하는 것이다. 예를 들어, 스팸이 아닌 메일을 스팸으로 잘못 분류하는 것은 매우 좋지 않다. 그러나 스팸 메일을 스팸이 아닌 메일로 잘못 분류하는 것은 기분은 좀 나쁘지만 작업의 끝은 아니다.
‘True vs. False’ and ‘Positive vs. Negative’
분류 모델의 예측을 평가하는 데에 사용할 수 있는 평가 지표와 예측에 대한 임계값 변경의 영향을 알아보자.
분류 모델을 평가하기 위해 주로 사용하는 지표를 알아보자.
모두가 알고 있는 ‘양치기 소년’ 이야기에 빗대어 정의를 해보면,
- ‘늑대가 있음’은 Positive
- ‘늑대가 없음’은 Negative
위의 두 정의를 사용하여, 모델이 ‘늑대 예측’을 하는 4 가지의 가능한 결과를 모두 나타내는 2x2 행렬로 나타낼 수 있다. 이를 confusion matrix라고 한다.
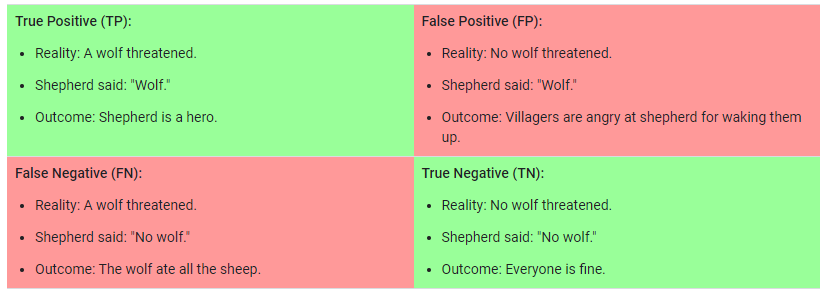
- True-Positive는 모델이 늑대가 있어서 ‘늑대가 있음’으로 올바르게 예측하는 결과이다.
- True-Negative는 모델이 늑대가 없어서 ‘늑대가 없음’으로 올바르게 예측하는 결과이다.
- False-Positive는 모델이 늑대가 없는데 ‘늑대가 있음’으로 잘못 예측하는 결과이다.
- False-Negative는 모델이 늑대가 있는데 ‘늑대가 없음’으로 잘못 예측하는 결과이다.
정확도 (Accuracy)
이 confusion matrix를 사용하여 분류 모델을 평가하는 방법을 알아보자.
정확도(Accuracy)는 분류 모델을 평가하기 위한 하나의 측정의 기준이다. 비공식적으로, 정확도는 모델이 올바르게 예측한 비율을 말한다. 공식적으로는 다음과 같이 정의한다.
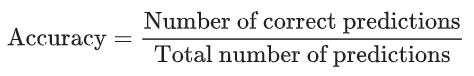
이진 분류에 대해서도, 정확도는 양수 및 음수에 관해서도 계산할 수 있다.
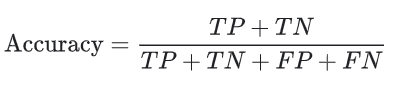
- TP = True-Positive
- TN = True-Negative
- FP = False-Positive
- FN = False-Negative
그렇다면 예를 들어, 악성 종양을 분류해내는 모델을 만든다고 할 때, 100개의 종양을 악성(positive) 또는 양성(negative)으로 분류한 다음 모델의 정확도를 계산해보자.
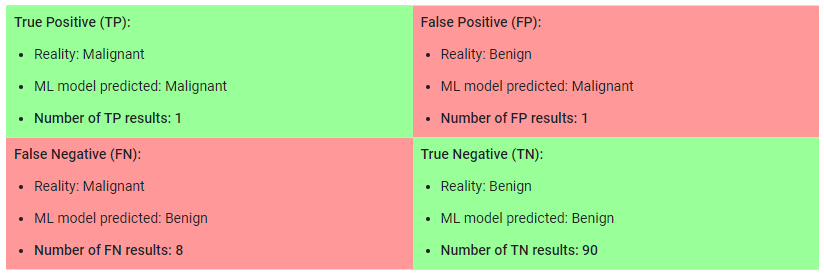
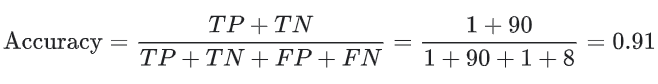
총 100개의 데이터 중 91개의 정확한 예측을 했기 때문에, 정확도는 0.91 또는 91%가 계산되었다. 이는 모델이 악성 종양을 식별하는 일을 훌륭하게 수행하고 있다는 것을 의미한다.
모델의 성능에 대한 이해를 높이기 위해 positive와 negative를 더 자세히 분석해보자.
100개의 종양 데이터 중 91개는 양성(90개의 TN, 1개의 FP) 데이터이고, 9개는 악성(1개의 TP, 8개의 FN) 데이터이다.
이에 대해, 모델은 91개의 양성 종양 중 90개를 양성으로 정확하게 식벌하였다. 그러나, 9개의 악성 종양 중 1개만 정확하게 식별하였다.
91%의 정확도는 높은 수치이다. 그러나 이 경우, 언뜻 보기에는 좋아 보일 수 있지만 항상 양성만을 예측하는 다른 분류 모델이 있다고 했을 때도 동일한 91%의 정확도를 달성한다. 즉, 이 모델은 악성 종양과 양성 종양을 구별하는 예측 성능이 0인 모델보다 나을 것이 없는 것이다.
이와 같이 positive 데이터의 수와 negative 데이터의 수가 불균형한 데이터 세트(악성과 양성 데이터 수의 차이가 큼)로 작업할 때, 정확도 만으로는 전체 성능을 알 수 없다.
정밀도 (Precision) and 재현율 (Recall)
그렇다면, Positive와 Negative 두 클래스의 불균형 문제를 평가하기 위헤, 더 나은 측정 기준인 정밀도와 재현율 이 두가지에 대해서 알아보자.
정밀도 (Precision)
정밀도는 다음 질문에 대한 답이다.
Positive라고 예측한 결과 중 실제로 Positive인 비율은 얼마인가?
정밀도는 다음과 같이 정의된다.
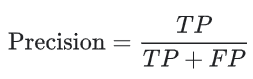
False-Positive를 생성하지 않는 모델의 정밀도는 1.0이다.
종양 분류 결과에 대한 정밀도를 계산해보자.

이 모델의 정밀도는 0.5이다. 즉, 종양이 악성이라고 예측할 때 50%의 정확도를 보인다는 것이다.
재현율 (Recall)
재현율은 다음 질문에 대한 답이다.
정확하게 예측한 결과 중 실제로 Positive인 비율은 얼마인가?
수학적으로는 다음과 같이 정의 된다.
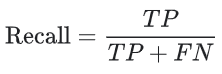
종양 분류 결과에 대한 재현율을 계산해보자.

이 모델의 재현율은 0.11이다. 즉, 모든 악성 종양의 11%를 정확하게 식별한다.
정밀도와 재현율 : 줄다리기 (A Tug of War)
모델의 효율성을 완전히 평가하기 위해서는 정밀도와 재현율을 모두 확인해야한다. 불행히도, 정밀도와 재현율은 종종 긴장관계에 있다. 즉, 정밀도를 개선하면 일반적으로 재현율은 감소하고, 재현율을 개선하면 정밀도가 감소한다.
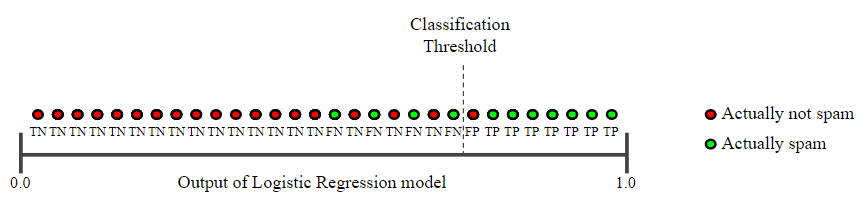
다음의 이메일 분류 모델이 예측한 30개의 결과를 통해 알아보자. 분류 임계값 오른쪽에 있는 항목은 ‘스팸’으로 분류되고, 왼쪽은 ‘스팸 아님’으로 분류된다.
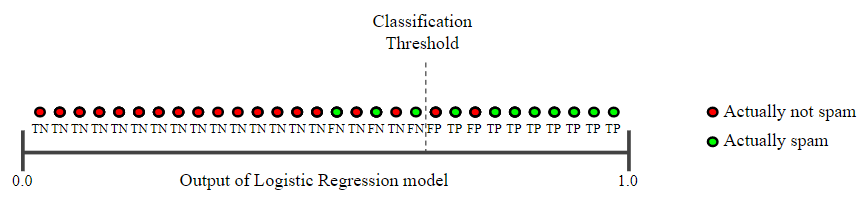
위의 그림에 대한 정밀도와 재현율을 계산해보자.

정밀도는 Positive라고 예측한 결과 중 실제로 Positive인 비율이라고 했다. 스팸 메일을 올바르게 ‘스팸’이라고 예측한 비율이다.
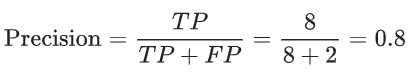
재현율은 정확하게 예측한 결과 중 실제로 Positive인 비율이라고 했다. ‘스팸’과 ‘스팸 아님’을 올바르게 예측한 결과 중 ‘스팸’의 비율이다.
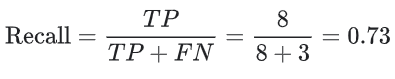
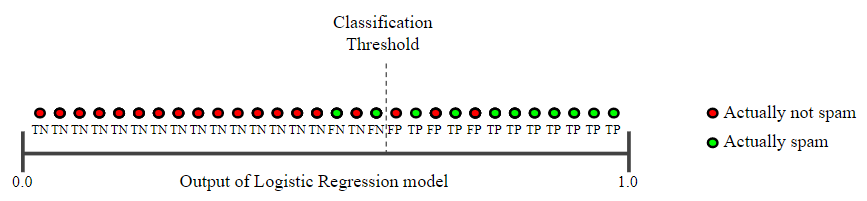
아래의 그림은 위의 그림보다 임계값을 높였을 때의 결과이다.
임계값을 보다 높은 값으로 설정했을 때, False-Positive은 감소하고 False-Negative는 증가한다. 결과적으로, 정밀도가 증가하고 재현율이 감소한다.

반대로, 임계값을 낮추면 어떻게 되는지 확인해보겠다.
임계값을 보다 낮은 값으로 설정했을 때, False-Positive은 증가하고 False-Negative는 감소한다. 결과적으로, 정밀도가 감소하고 재현율이 증가한다.

이렇게 정밀도와 재현율은 종종 마치 줄다리기 관계에 있는 경우가 많다. 상황에 따라서 정밀도에 더 초점을 맞출 것인지, 재현율에 더 초점을 맞출 것인지 잘 고려하여 모델을 활용할 수 있다.
또한, F1-score와 같은 정밀도와 재현율 모두에 의존하는 다양한 측정 기준이 개발되었다.
ROC Curve and AUC
ROC curve
ROC curve(Receiver Operating Characteristic curve)는 모든 임계값에 대한 분류 모델의 성능을 보여주는 그래프이다. 이 곡선은 두 개의 매개변수를 표시한다.
- TPR : True-Positive Rate
- FPR : False-Positive Rate
TPR은 재현율과 동의어이다. 따라서 다음과 같이 정의된다.
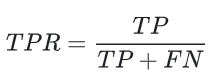
FPR은 다음과 같이 정의된다.
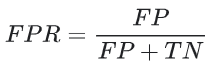
ROC curve는 다양한 분류 임계값에 대한 TPR vs. FPR을 나타낸다. 분류 임계값을 낮추면 더 많은 데이터들이 Positive로 분류되기 때문에, FP와 TP가 모두 증가한다. 다음 그림은 일반적인 ROC curve 이다.
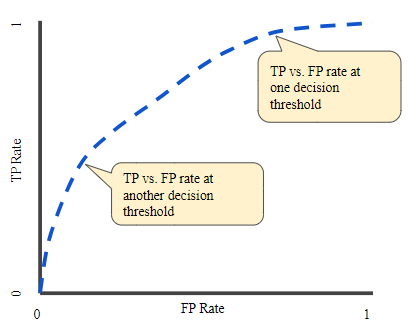
ROC curve의 점들을 계산하기 위해, 다양한 분류 임계값으로 로지스틱 회귀 모델을 여러 번 평가하는 방법이 있다. 하지만 이 방법은 비효율적이다. 따라서, 정렬 기반 알고리즘을 사용하여 알아낸다. 이것을 AUC라고 부른다.
AUC : Area Under the ROC curve
AUC는 ‘ROC curve의 아래 영역’을 말한다. 즉, AUC는 (0, 0)에서 (1, 1)까지 전체 ROC curve 아래의 모든 2차원 영역을 측정한다.
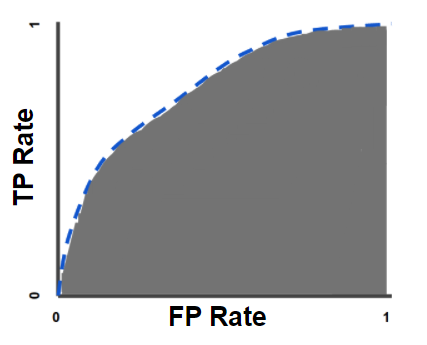
AUC는 가능한 모든 분류 임계값에 대한 종합적인 성능의 측정값을 제공한다. AUC를 해석하는 한 가지 방법은 모델이 무작위 Negative 데이터 보다 무작위 Positive 데이터를 더 높게 평가할 확률이다. 예를 들어, 아래의 그림 처럼, 로지스틱 회귀 예측이 왼쪽에서 오른쪽으로 오름차순으로 정렬되어 있다고 가정하자.

AUC는 임의의 Positive 데이터(녹색)가 임의의 Negative 데이터(적색)의 오른쪽에 배치될 확률을 나타낸다.
AUC 값의 범위는 0 에서 1 이다. 예측이 100% 잘못된 모델의 AUC는 0.0 이고, 예측이 100% 정확한 모델의 AUC는 1.0 이다.
AUC는 다음의 두 이유로 가치가 있다.
- AUC는 척도가 변하지 않는다. 예측의 절대값이 아니라 예측을 얼마나 잘 하는지 등급을 매기는 것이다.
- AUC는 분류 임계값이 변하지 않는다. 어떤 분류 임계값이 적용되었는지에 관계없이 모델의 예측의 품질을 측정한다.
그러나, 다음의 두 사항에는 AUC의 유용성을 제한할 수 있다.
- 척도가 변하지 않는 것이 항상 바람직한 것은 아니다. 예를 들어, 때로는 보정된 확률의 출력값이 필요한데 AUC로 그것에 대해서는 알 수 없다.
- 분류 임계값이 변하지 않는 것이 항상 바람직한 것은 아니다. False Negative와 False Positive 값의 사이에 큰 차이가 있을 경우, 둘 중 한 가지의 분류 오류를 최소화하는 것이 중요할 수 있다. 예를 들어, 이메일 스팸 탐지에서, 비록 False Negative가 증가 하더라도 False Positive를 최소화하는 것을 우선할 수 있다. AUC는 이러한 유형의 최적화에 유용한 측정 기준이 아니다.
예측 편향 (Prediction Bias)
로지스틱 회귀 예측은 편향되어서는 안된다.
"예측의 평균"은 ≈ "관측의 평균"이어야 한다.
"average of predictions" should ≈ "average of observations"
예측 편향은 두 평균이 얼마나 떨어져 있는지 측정하는 양이다.

참고로 여기서 다루는 ‘예측 편향’은 편향(wx + b의 b)와 다르다.
의미있는 0 이아닌 예측 편향은 모델의 어딘가에 버그가 있다는 것을 알려준다. 이는 Positive 레이블이 얼마나 자주 발생하는지에 대해 모델이 잘못되었음을 나타내기 때문이다.
예를 들어, 평균적으로 모든 이메일의 1%가 스팸 메일이라는 것을 알고있다고 하자. 그러면 새로 주어진 이메일 데이터 세트에 대해 전혀 모르는 경우, 스팸일 가능성이 1%라고 예측할 것이다. 마친가지로, 좋은 스팸 분류 모델은 평균적으로 이메일이 스팸일 가능성이 1%라고 예측해야 한다. 그러나 모델의 평균 예측이 스팸일 가능성이 20%라고 나왔다면, 예측 편향이 있다고 결론을 내릴 수 있는 것이다.
예측 편향이 나타날 수 있는 근본 원인은 다음과 같다.
- 불완전한 특성 세트
- 노이즈가 낀 데이터 세트
- 버그가 있는 파이프라인
- 편향된 training 샘플
- 지나치게 강력한 정규화
일단 모델을 학습시킨 후, 사후 처리로 예측 편향을 정정하면 된다고 생각할 수도 있다. 예를 들어, 모델에 +3%의 편향이 있는 경우 평균 예측을 3% 낮추는 보정 레이어를 추가할 수 있다. 그러나, 다음과 같은 이유로 보정 레이어를 추가하는 것은 좋지 않다.
- 증상보다 원인을 고쳐야한다.
- 계속 업데이트 해야 하는 불안정한 모델을 구축했다.
가능하면 보정 레이어는 피해야한다. 보정 레이어를 사용하는 프로젝트는 모델의 모든 잘못을 수정하기 위해 보정 레이어에 의존하는 경향이 있다. 따라서 궁극적으로, 보정 레이어를 유지 및 관리하는 것은 악몽이 될 수 있다.
좋은 모델은 일반적으로 편향이 거의 0에 가깝다. 즉, 예측 편향이 낮다고 해서 모델이 좋은 것은 아니다. 정말 끔찍한 모델은 예측 편향이 0일 수 있다. 예를 들어, 모든 데이터의 평균값만 예측하는 모델은 편향이 0이더라도 잘못된 모델이 된다.
Bucketing and Prediction Bias
로지스틱 회귀는 0 과 1 사이의 값을 예측한다고 했다. 그러나 레이블이 지정된 모든 데이터는 정확히 0 또는 1 이다. 예를 들어, ‘스팸 아님’은 0으로 레이블링 되고, ‘스팸’은 1로 레이블링된다. 그러므로 예측 편향을 조사할 때, 한 가지의 데이터 만으로는 예측 편향을 정확하게 측정할 수 없다. 따라서 데이터의 ‘bucket’에 대한 편향을 조사해야 한다. 즉, 로지스틱 회귀에 대한 예측 편향은 예측값(모델이 예측한 값)을 관찰값(실제 데이터의 값)과 비교할 수 있도록 충분한 수의 데이터를 함께 그룹화할 때만 의미가 있다.
bucket은 다음과 같은 방법으로 형성할 수 있다.
- 타겟 예측을 선형으로 분할한다.
- 분위수를 형성한다.
아래의 특정 모델에 대한 그래프를 보자. 각 점은 1,000개의 값에 대한 bucket을 나타낸다.
- x축은 해당 bucket에 대해 모델이 예측한 평균을 나타낸다.
- y축은 해당 bucket에 대한 데이터 세트 값의 실제 평균을 나타낸다.
양 축 모두 로그스케일을 적용하였다.
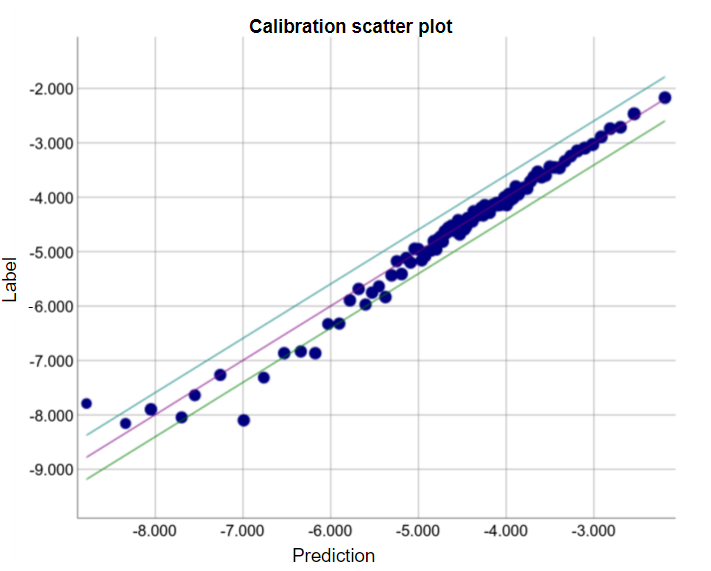
모델의 일부에 대해서만 예측이 좋지 않다. 왜 그럴까?
- training set는 데이터 공간의 특정 하위 집합을 충분히 나타내지 못한다.
- 데이터 세트의 일부 하위 집합은 다른 하위 집합보다 노이즈가 많다.
- 모델이 지나치게 정규화되었다. (람다 값을 줄이는 것을 고려해야한다.)
※ 참고
Google Developer - Thresholding
Google Developer - True vs. False and Positive vs. Negative
Google Developer - Accuracy
Google Developer - Precision and Recall
Google Developer - ROC Curve and AUC
Google Developer - Prediction Bias
